Three shape coding techniques are shortly introduced. All of them are computed from the contour of an object. The object is expected to be the ordered (x,y) presentation of the contour pixels.
The chain code histogram (CCH) is meant to group together objects that look similar to a human observer [10]. It is not meant for exact detection and classification tasks. The CCH is calculated from the chain code presentation of a contour.
The Freeman chain code [6] is a compact way to represent a
contour of an object. The chain code is an ordered sequence of n
links 
, where 
is a vector connecting
neighboring contour pixels. The directions of are coded with integer
values k=0,1,...,K-1 in a counterclockwise sense starting from the
direction of the positive x-axis. The number of directions K takes
integer values 
where M is a positive integer. The chain
codes where K>8 are called generalized chain codes [5].
The calculation of the chain code histogram is fast and simple. The CCH is a discrete function
where 
is the number of chain code values k in a chain code,
and n is the number of links in a chain code.
A simple example is depicted in Figure 1.
In Figure 1(a) are the directions of the eight connected
chain code.
In Figure 1(b) is a sample object, a square. The starting
point for the chain coding is marked with a black circle, and the
chain coding direction is clockwise.
In Figures 1(c)-(d) are the chain code and the CCH of
the contour of the square.
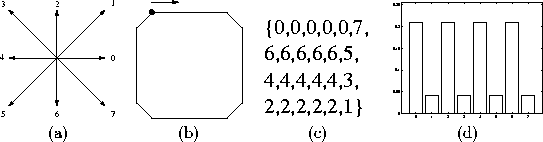
Figure 1: (a) The directions of the eight connected chain code (K=8).
(b) A sample object, a square, (c) chain code
presentation of the square, and (d) the chain code histogram
of the square.
The CCH is a translation and scale invariant shape descriptor.
It can be made invariant to rotations of 
because the
rotation causes only a circular shift in the CCH.
To achieve better rotation invariance the normalized chain code
histogram (NCCH) should be used [10].
It takes into account the lengths of different directions.
The pairwise geometric histogram (PGH) is a powerful shape descriptor that is applied to polygonal shapes [4, 2]. It can be applied also to an irregular shape if the shape is first approximated with a polygon. For a recent review of polygon approximation algorithms, see for example [19].
Consider a polygon defined by its edgepoints
.
Now successive edgepoints define the line segments the polygon consists of.
The PGH is calculated using the following strategy: Let each line segment
be a reference line on its turn. Then the relative angle 
and the perpendicular minimum and maximum distances ( 
and
) are calculated between the reference
line and all the other lines, as shown in Figure 2(a).
The histogram values are increased by one on the indexes corresponding
to the angle 
and the line segment from the to
(Figure 2(b)).
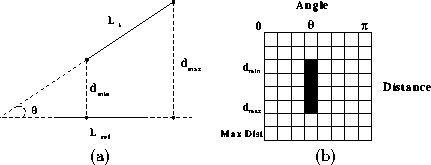
Figure 2: (a) Relative angle and perpendicular distances between two
lines, and (b) the pairwise geometric histogram.
A new scheme to reduce the size of the PGH is proposed.
Conditional expectations of each row and
column are calculated and collected into a feature vector.
Let p(i,j) be the PGH value in the position (i,j).
Then the feature vector 
is given as
where N is the number of rows of the PGH, M is the number of
columns of the PGH,
is the conditional expectation of the ith row,
and 
is the conditional expectation of the jth column,
Thus the number of features is reduced from NM to N+M. This presents significant savings in calculation time and memory requirements, especially if N and M are large.
In this section, five simple shape descriptors
are introduced (Figure 3).
Variations of most of them have been widely used in object recognition
[12, 17]. Each descriptor alone is insufficient for a
complex recognition task, but the combination of them is shown to have
good recognition capabilities (Section 3).
All these shape descriptors require only
calculation steps expect convexity which requires
calculation steps.
For a more profound discussion and definitions of
these descriptors, see [15].
Figure 3: Five simple shape descriptors.
Convexity can be defined as the ratio of perimeters of the convex hull of the contour and the original contour. The convex hull is the minimal convex covering of an object. The algorithm for constructing a convex hull involves traversing the contour and minimizing turn angle in each step. Practically, dot product can be maximized instead.
Principal axes of an object can be uniquely defined as segments of lines crossing each other orthogonally in the centroid of the object and representing the directions with zero cross-correlation. This way, a contour is seen as an realization of a statistical distribution. The ratio of principal axis can be calculated from the covariance matrix of a contour. It is not necessary to calculate actual eigenvectors nor eigenvalues.
Compactness is often defined as the ratio of squared perimeter and the area of an object. It reaches the minimum in a circular object and approaches infinity in thin, complex objects. The measure applied in this paper is the ratio of the perimeter of a circle with equal area as the original object and the original perimeter.
Sometimes a shape should be compared against a template. A circle is an obvious and general template choice. The circular variance is the proportional mean-squared error with respect to solid circle. It gives zero for a perfect circle and increases along shape complexity and elongation.
Elliptic variance is defined similarly to the circular variance. An ellipse is fitted to the shape (instead of a circle) and the mean-squared error is measured.
