
On this page, the structure of SOM and the SOM algorithm are described.
A SOM is formed of neurons located on a regular, usually 1- or 2-dimensional grid. Also higher dimensional grids are possible, but they are not generally used since their visualization is much more problematic.
The neurons are connected to adjacent neurons by a neighborhood relation dictating the structure of the map. In the 2-dimensional case the neurons of the map can be arranged either on a rectangular or a hexagonal lattice, see Figure 1. If the sides of the map are connected to each other, the global shape of the map becomes a cylinder or a toroid, see figure Figure 2.
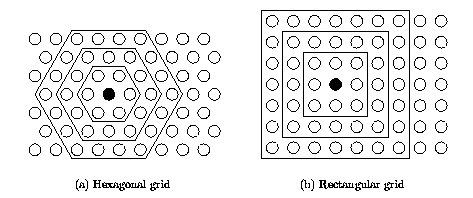 |
| Figure 1: Neighborhoods (size 1, 2 and 3) of the unit marked with black dot: (a) hexagonal lattice, (b) rectangular lattice. |
 |
| Figure 2: Different map shapes: sheet on the left, cylinder in the center and toroid on the right. In the two latter, the connections across the gaps exist. They just have not been drawn. |
Each neuron i of the SOM has an associated d-dimensional prototype (aka weight, reference, codebook or model) vector mi = [mi1 mi2 ... mid], where d is equal to the dimension of the input vectors.
Each neuron has actually two positions: one in the input space -- the prototype vector -- and another in the output space -- on the map grid. Thus, SOM is a vector projection method defining a nonlinear projection from the input space to a lower-dimensional output space. On the other hand, during the training the prototype vectors move so that they follow the probability density of the input data. Thus, SOM is also a vector quantization algorithm. Simplified, SOM is nothing more than an algorithm that combines these two tasks: vector quantization and projection.
Immediate neighbors, the neurons that are adjacent, belong to the 1-neighborhood Ni1 of the neuron i. Neighborhoods of different sizes in rectangular and hexagonal lattices are illustrated in Figure 1. The innermost polygon corresponds to 1-neighborhood, the second to the 2-neighborhood and the biggest to the 3-neighborhood.
The neighborhood function determines how strongly the neurons are connected to each other. The simplest neighborhood function is the bubble: it is constant over the whole neighborhood of the winner unit and zero elsewhere. Another is the Gaussian neighborhood function
![]() , where rc is the location of unit c on the map grid
and the sigma(t) is the neighborhood radius at time t.
, where rc is the location of unit c on the map grid
and the sigma(t) is the neighborhood radius at time t.
Neighborhood function and the number of neurons determine the granularity of the resulting mapping. The larger the area where neighborhood function has high values, the more rigid is the map. The larger the map, the more flexible it can become. This interplay determines the accuracy and generalization capability of the SOM.
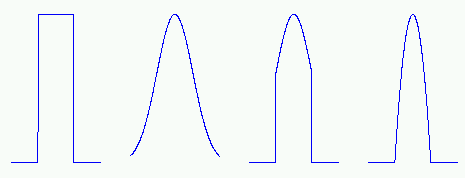 |
| Figure 3: The four neighborhood functions in SOM Toolbox: bubble, gaussian, cut gaussian and epanechicov (which is essentially max(0,1-x2)). |
In the classical SOM, the number of neurons and their topological relations are fixed from the beginning. There are four issues which need to decided: the number of neurons, dimensions of the map grid, map lattice and shape.
The number of neurons should usually be selected as big as possible, with the neighborhood size controlling the smoothness and generalization of the mapping. The mapping does not considerably suffer even when the number of neurons exceeds the number of input vectors, if only the neighborhood size is selected appropriately. However, as the size of the map increases e.g. to tens of thousands of neurons the training phase becomes computationally impractically heavy for most applications.
If possible, the shape of the map grid should correspond to the shape of the data manifold. Therefore, the use of toroid and cylinder shapes is only recommended if the data is known to be circular. For the default sheet shaped map, it is recommended that side length along one dimension is longer than the others, e.g. msize = [15 10], so that the map can orientate itself properly. One could possibly use the eigenvalues of the training data set as a guideline in setting the map grid side lengths.
The use of hexagonal lattice is usually recommended, because then all 6 neighbors of a neuron are at the same distance (as opposed to the 8 neighbors in a rectangular lattice). This way the maps become smoother and more pleasing to the eye. However, this is mostly a matter of taste.
Before the training, initial values are given to the prototype vectors. The SOM is very robust with respect to the initialization, but properly accomplished it allows the algorithm to converge faster to a good solution. Typically one of the three following initialization procedures is used:
In each training step, one sample vector x from the input data set is chosen randomly and a similarity measure is calculated between it and all the weight vectors of the map. The Best-Matching Unit (BMU), denoted as c, is the unit whose weight vector has the greatest similarity with the input sample x. The similarity is usually defined by means of a distance measure, typically Euclidian distance. Formally the BMU is defined as the neuron for which
||x - mc|| = mini{||x - mi||},
where ||.|| is the distance measure.
After finding the BMU, the prototype vectors of the SOM are updated. The prototype vectors of the BMU and its topological neighbors are moved closer to the input vector in the input space. This adaptation procedure stretches the prototypes of the BMU and its topological neighbors towards the sample vector. This is illustrated in Figure 4. The SOM update rule for the weight vector of the unit i is:
mi(t+1) = mi + a(t) hci(r(t)) [x(t) - mi(t)],
where t denotes time, a(t) is learning rate and hci(r(t)) the neighborhood kernel around the winner unit c, with neighborhood radius r(t).
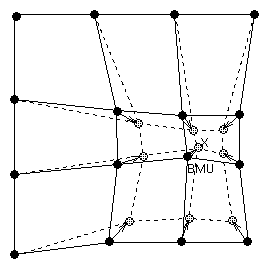 |
| Figure 4: Updating the best matching unit (BMU) and its neighbors towards the input sample marked with x. The solid and dashed lines correspond to situation before and after updating, respectively. |
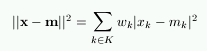
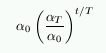
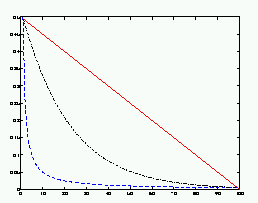 |
| Figure 5: The three learning rate functions in SOM Toolbox: linear (red), power series (black) and inverse-of-time (blue). |
Also neighborhood radius typically decreases with time. Since large neighborhood radius makes the SOM more rigid, it is usually used in the beginning of training, and then it is gradually decreased to a suitable final radius. A suitable final radius is, for example, one. Notice that if neighborhood radius is set to zero r=0, the SOM algorithm reduces to k-means algorithm.
The total training time -- or, the number of samples presented to the SOM --- is an important consideration. The number of training steps should be at least 10 times the number of map units.
The training is usually performed in two phases. In the first phase, relatively large initial learning rate and neighborhood radius are used. In the second phase both learning rate and neighborhood radius are small right from the beginning. This procedure corresponds to first tuning the SOM approximately to the same space as the input data and then fine-tuning the map. If the linear initialization procedure is used the first training phase can be skipped.
An important variant of the basic SOM is the batch algorithm. In it, the whole training set is gone through at once and only after this the map is updated with the net effect of all the samples. Actually, the updating is done by simply replacing the prototype vector with a weighted average over the samples, where the weighting factors are the neighborhood function values.
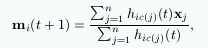
where c(j) is the BMU of sample vector xj, hi,c(j) the neighborhood function (the weighting factor), and n is the number of sample vectors.
There are many variants to the basic SOM. One variantion theme is to use neuron-specific learning rates and neighborhood sizes. Another is to use adaptive or flexible neighborhood definitions or even growing map structures. The goal of these variations is to enable the SOM to follow better the topology of the underlying data set or to achieve better quantization results. A usual defect of these methods is that the visualization properties suffer or that the algorithm becomes computationally heavier. Another family of variations aims at making the SOM a better classifier.
You are at: CIS → SOM Toolbox: implementation of the algorithm
Page maintained by webmaster@cis.hut.fi, last updated Friday, 18-Mar-2005 16:23:05 EET