
The SOM is a new, effective software tool for the visualization of high-dimensional data. It converts complex, nonlinear statistical relationships between high-dimensional data items into simple geometric relationships on a low-dimensional display. As it thereby compresses information while preserving the most important topological and metric relationships of the primary data items on the display, it may also be thought to produce some kind of abstractions. These two aspects, visualization and abstraction, can be utilized in a number of ways in complex tasks such as process analysis, machine perception, control, and communication.
The SOM usually consists of a two-dimensional regular grid of nodes. A model of some observation is associated with each node (cf. Fig. 1).

Figure 1: In this exemplary application, each processing
element in the hexagonal grid holds a model of a short-time spectrum
of natural speech (Finnish). Notice that neighboring models are
mutually similar.
The SOM algorithm computes the models so that they optimally describe the domain of (discrete or continuously distributed) observations.
The models are organized into a meaningful two-dimensional order in which similar models are closer to each other in the grid than the more dissimilar ones. In this sense the SOM is a similarity graph, and a clustering diagram, too. Its computation is a nonparametric, recursive regression process.
Regression of an ordered set of model vectors ![]() into the space of observation vectors
into the space of observation vectors ![]() is often made by the following process:
is often made by the following process:
![]()
where t is the sample index of the regression step, whereby
the regression is performed recursively for each presentation of a
sample of ![]() . Index c
(``winner'') is defined by the condition
. Index c
(``winner'') is defined by the condition
![]()
Here ![]() is called the
neighborhood function, and it is like a smoothing kernel that
is time-variable and its location depends on condition in equation
(2). It is a decreasing function of the distance between the the
ith and cth models on the map grid.
is called the
neighborhood function, and it is like a smoothing kernel that
is time-variable and its location depends on condition in equation
(2). It is a decreasing function of the distance between the the
ith and cth models on the map grid.
The neighborhood function is often taken to be the Gaussian
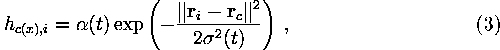
where ![]() is the learning-rate
factor, which decreases monotonically with the regression steps,
is the learning-rate
factor, which decreases monotonically with the regression steps, ![]() and
and ![]() are the vectorial
locations in the display grid, and
are the vectorial
locations in the display grid, and ![]() corresponds to the width of the neighborhood function, which is also
decreasing monotonically with the regression steps.
corresponds to the width of the neighborhood function, which is also
decreasing monotonically with the regression steps.
A simpler definition of ![]() is the following:
is the following:
![]() if
if ![]() is smaller than a
given radius around node c (whereby this radius is a
monotonically decreasing function of the regression steps, too), but
otherwise
is smaller than a
given radius around node c (whereby this radius is a
monotonically decreasing function of the regression steps, too), but
otherwise ![]() . In this case we
shall call the set of nodes that lie within the given radius the
neighborhood set
. In this case we
shall call the set of nodes that lie within the given radius the
neighborhood set ![]() .
.
Due to the many stages in the development of the SOM method and its variations, there is often useless historical ballast in the computations.
For instance, one old ineffective principle is random
initialization of the model vectors ![]() . Random
initialization was originally used to show that there exists a strong
self-organizing tendency in the SOM, so that the order can even emerge
when starting from a completely unordered state, but this need not be
demonstrated every time. On the contrary, if the initial values for
the model vectors are selected as a regular array of vectorial values
that lie on the subspace spanned by the eigenvectors corresponding to
the two largest principal components of input data, computation of the
SOM can be made orders of magnitude faster, since (i) the SOM is then
already approximately organized in the beginning, (ii) one can start
with a narrower neighborhood function and smaller learning-rate
factor.
. Random
initialization was originally used to show that there exists a strong
self-organizing tendency in the SOM, so that the order can even emerge
when starting from a completely unordered state, but this need not be
demonstrated every time. On the contrary, if the initial values for
the model vectors are selected as a regular array of vectorial values
that lie on the subspace spanned by the eigenvectors corresponding to
the two largest principal components of input data, computation of the
SOM can be made orders of magnitude faster, since (i) the SOM is then
already approximately organized in the beginning, (ii) one can start
with a narrower neighborhood function and smaller learning-rate
factor.
Many computational aspects like this have been discussed in the software package SOM_PAK [1], as well as the book [2].
Another remark concerns faster algorithms. The incremental regression process defined by equations (1) and (2) can often be replaced by the following batch computation version which, especially with Matlab functions, is significantly faster.
If all observation samples ![]() are available prior to
computations, they can be applied as a batch in the regression,
whereby the following computational scheme can be used [2]:
are available prior to
computations, they can be applied as a batch in the regression,
whereby the following computational scheme can be used [2]:
Notice that steps 2 and 3 need less memory if at step 2 we only
make lists of the observation samples ![]() at
those units that have been selected for winner, and at step 3 we form
the mean over the union of the lists that belong to the
neighborhood set
at
those units that have been selected for winner, and at step 3 we form
the mean over the union of the lists that belong to the
neighborhood set ![]() of unit i.
of unit i.
Finally it should be taken into account that the purpose of the SOM is usually visualization of data spaces. For an improved quality (isotropy) of the display it is advisable to select the grid of the SOM units as hexagonal; the reason is similar as when using a hexagonal halftone raster for images.
The above algorithms can often be generalized by defining various generalized matching criteria.
The following categories of similarity graphs, computed by the SOM, have already been used in many practical applications:
A list of research papers from very different application areas of the SOM and its variations is available in the Internet at the WWW address http://www.cis.hut.fi/research/som-bibl/.
[1] Kohonen, T., Hynninen, J., Kangas, J., Laaksonen, J. (1996). SOM_PAK: The self-organizing map program package. Report A31. Helsinki University of Technology, Laboratory of Computer and Information Science, Espoo, Finland. Also available in the Internet at the address http://www.cis.hut.fi/research/som_lvq_pak.shtml.
[2] Kohonen, T. (1995). Self-Organizing Maps. Series in Information Sciences, Vol. 30. Springer, Heidelberg. Second ed. 1997.
You are at: CIS → SOM Toolbox: Intro to SOM by Teuvo Kohonen
Page maintained by webmaster@cis.hut.fi, last updated Friday, 18-Mar-2005 15:53:37 EET