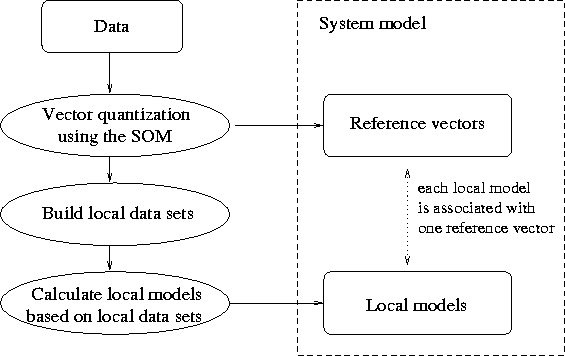
Figure 3.2: A batch algorithm scheme for constructing and testing local models.
A traditional way to approach modeling is to estimate the underlying function globally. In the last decade, however, local models have been a source of much interest because in many cases they give better results than global models [40]. This is especially true if the function characteristics vary throughout the feature space. The local models can be constructed in various ways ranging from using the best example vector as such to splines and small MLPs. Usually, local models are kept simple such as weighted averages of the example vectors or linear regression models.
With the SOM, the local models are usually constructed for each unit separately. They can be either trained simultaniously with the SOM using an iterative procedure as in [35], or with a batch algorithm after the SOM has been trained [50]. A scheme for constructing and testing the local models using a batch algorithm is depicted in figure 3.2.

Figure 3.2: A batch algorithm scheme for constructing and testing
local models.
Based on the data set, the data space is quantized. Local data sets are then constructed for each of the reference vectors: the local data set of a reference vector is formed of the data vectors falling to the vector's Voronoi region. If a local data set of a reference vector is considered too small, it can be augmented from the data sets of similar, close lying reference vectors. At the last step, local models are constructed based on the local data sets. The local models are used by selecting the best-matching reference vector and using the corresponding local model.