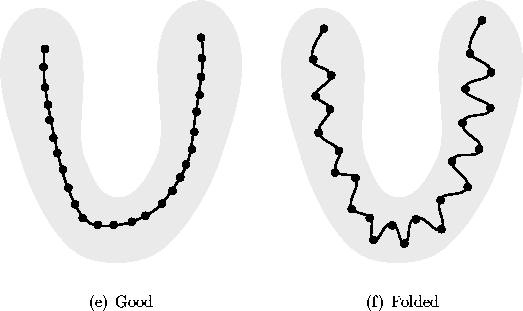
Figure 2.4: A topologically good (a) and a folded 1-dimensional SOM (b).
The SOM combines the properties of vector quantization and data projection techniques. It searches for good reference vectors and at the same time orders them on a regular grid. The grid can be thought of as a 2-dimensional elastic network following the distribution of the data.
The SOM does not, as projection methods in general, try to preserve the distances directly but rather the topology or local structure of the input data. Thus, the interpretation of the SOM should be done predominantly locally [16].
The goals of vector quantization and topology preservation sometimes become contradictory and the SOM has to find a balance between them. An example is shown in figure 2.4. To better approximate the distribution of the input data, the SOM makes twists and turns which correspond poorly to the actual topology of the data set. The balance between quantization accuracy and topological ordering can be controlled with the radius of the neighborhood kernel. Note that if the neighborhood radius is set to zero, the SOM reduces to a pure vector quantization algorithm.

Figure 2.4: A topologically good (a) and a folded 1-dimensional SOM (b).
The combination of vector quantization and data projection can also be done sequentially rather than simultaniously as in the SOM. The curvilinear component analysis is a manifestation of this approach [6]. It is a two-layer method where the first layer performs vector quantization and the second layer projects the quantized vectors nonlinearly to a lower-dimensional output space.