Tik-61.183 Special course on information technology III
Randomized algorithmsSpring 2000
Heikki Mannila
Exercises 1, due February 9, 2000
- 1.
- The variance D2(X) of a random variable X is
the expectation of the random variable
(X-E(X))2,
i.e.,
D2(X) = E((X-E(X))2).
The variance is also denoted by
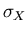 ,
or by var[X].
Show that
D2(X) = E(X2) - (E(X))2.
,
or by var[X].
Show that
D2(X) = E(X2) - (E(X))2.
- 2.
- Let X(n) be the number of tails obtained when flipping a fair coin n times. What is E(X(n))? What is D2(X(n))?
- 3.
- Let X(n,p) be the number of heads obtained when flipping a biased coin (probability of head = p) n times. Compute E(X(n,p)) and D2(X(n,p)).
- 4.
- Find Markov's inequality from a textbook and give an informal justification of it. State Chebyshev's inequality.
- 5.
- Approximate (either analytically or by simulation) the probability of the following event: ``When flipping a fair coin 1000 times, the number of heads is less than 450''.
http://www.cis.hut.fi/Opinnot/T-61.6030/k2000/exercises/1/exercise1.shtml
jkseppan@mail.cis.hut.fi
Wednesday, 09-Feb-2000 20:47:36 EET