This chapter is not a substitute for the detailed information in the rest of this Guide, but it does summarize some important terms and concepts that may be new to you if you have not used a scientific visualization application before. So we suggest the following:
The printed documentation contains detailed information, including graphics, sample code, and data examples.
Many of the terms used in Data Explorer are borrowed from traditional scientific disciplines, others come from computer graphics, and a few have been coined by the Data Explorer software developers for lack of any widely accepted term. Important Data Explorer terms are defined in the Glossary.
The process of rendering an image involves a computer calculation of the amount of light falling on each visible surface of the objects in the "scene," as seen from the point of view of the computer "camera" (the viewer's eye point). During the rendering process, surface properties of objects are taken into account as are the colors of both the objects and the "lights" shining on them. In other words, a computer graphics renderer samples the scene in front of the camera at the resolution of the computer monitor on which the scene is to be displayed. Its sample space is the 3-dimensional "world" containing the objects. But the image renderer does not create a 3-dimensional picture; it only calculates the colors of the dots that can be seen on the 2-dimensional monitor screen from the chosen point of view. Any parts of objects that cannot be seen from that point of view are neither sampled nor rendered, nor are they stored in the image file or displayed on the monitor. This 2-dimensional image may appear 3-dimensional to our eyes because of shading, occlusion of distant objects by closer ones, and other visual cues that, in the real world, indicate dimensionality. Like any image, it is a representation, however real it may appear.
The concept of sampling should be familiar to anyone who has ever collected data on some kind of grid. For example, a botanist may lay down a series of square grid markers over an area of interest then count the numbers of species of grasses growing inside each grid square. The number so collected becomes a sample value or datum associated with that grid marker. A single number like this, whether floating point or integer, is called a scalar. If the wind velocity and direction at, say, the center of each grid square is also measured, the botanist would record a vector quantity as a second datum sampled at the same place. A vector encodes both direction and magnitude with two or more numeric "vector components."
In this example, the locations of the corners of each grid marker are recorded as an array of 2-dimensional coordinates that define the sampling area dimensions and the sampling resolution. In computer graphics terms, these spatial location points are called vertices (singular: vertex); in Data Explorer, they are referred to as "positions". Loosely, everyone calls them "points."
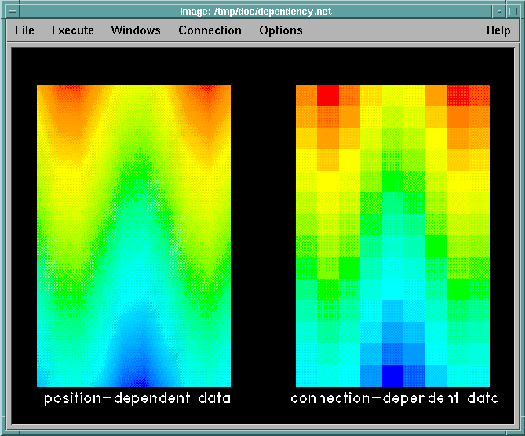
Four coordinate positions can be connected by a quadrilateral to define a grid element. The quadrilateral itself is called a connection in Data Explorer (we will discuss other connection types in a moment). Since the botanist collected one set of data per grid element, such data are termed connection-dependent data. This implies that the data value is assumed by Data Explorer to be constant within that element.
Consider another technique for data sampling: on a larger scale, remote-sensing satellites can resolve various features of the Earth down to some finite level of resolution. In this case, the grid positions are identified by a latitude-longitude coordinate pair, and the data values may encode such things as surface reflectance in the ultraviolet. By associating each data value with a latitude-longitude position, we produce position-dependent data.
This implies that data values should be interpolated between positions, using the connections (grid) if one is present. Data Explorer works equally well with position-dependent and connection-dependent data (see Figure 1).
Figure 1. Examples of
Data Dependency
We can extend our data sampling into three dimensions where appropriate. In that case, we identify each grid position with three coordinates. These coordinates form the corners of "volumetric" elements and the entire sample space is called a volume. A volumetric element may be a rectangular prism (like a cube) or a tetrahedron (a solid with four triangular faces, not necessarily equilateral).
In the cases just discussed, we made the implicit assumption that there is a logical connectivity between adjacent members of our 2-dimensional or 3-dimensional grid positions. The path connecting grid positions is called a connection in Data Explorer. For a surface (2- or 3-dimensional positions connected by 2-dimensional connections), we could choose to make triangular or quadrilateral connections (i.e., triangles or quads). Quads require four positions for each connection and triangles three. Data Explorer supports these element types as well as cubes, tetrahedra, and lines.
Suppose we first choose to link adjacent positions in the botanist's sample area with line connections. The grid markers were 1 meter on a side. Given a sampling area of 5 meters by 3 meters, the entire sample would be 15 meters square; there would be 24 positions (6 in X, and 4 in Y). On such a plot, we see that a position located at [x=0,y=0] is connected to its neighbor at [x=1,y=0]. We can imagine that it is meaningful to draw associations between data values at adjacent grid positions considering that so many natural phenomena are continuous rather than discrete. We assume that the grasses are free to spread across the area and the wind is free to blow in any direction over the area.
Previously, we assumed that samples were measured at the center of each grid square; that is, the botanist used quad connections to associate sets of four positions into 4-sided elements, then measured data values at the center of each connection element, yielding connection-dependent data. Now, assume that the botanist measures temperature values at each grid position. Temperature would then be position-dependent data. It's perfectly acceptable to have both kinds of data in the same data set. We will see how this works when we discuss Fields.
Assume that the first grid position (sampling point) lies precisely at the position coordinate [x=0,y=0]. We take a measurement and record the value. Then we measure the temperature at [x=1,y=0]. Later, we ask, what was the temperature at [x=0.5,y=0]? Quite honestly, we do not know, because our sampling resolution was not fine enough for us to give a definitive answer. However, if we make the assumption (very often, a perfectly reasonable assumption, but not always!) that our grid overlaid a continuous set of values, we can derive the expected data value by interpolation between known values. If we use line connections to connect adjacent points, we realize by looking at our mesh that a straight line connects the grid point [x=0,y=0] and [x=1,y=0] and that halfway along this line lies the grid point [x=0.5,y=0]. We can further assume that the data value at this midpoint is the average of the data values at known sample points bordering this location. By linear interpolation, we calculate a reasonable value for the temperature at [x=0.5,y=0].
We need to define polygonal connections over the 2-D grid if we wish to find the value at the point [x=0.2,y=0.7]. With line connections between adjacent pairs of grid points, we can only reasonably perform interpolations along those linear boundaries but not into the middle of our grid elements. By defining areas bounded by three or more points, we can perform interpolation across the area (the polygon surface) using weighting functions that take into account the data values at all points surrounding the area. In fact, this is the same process used by an image-rendering program: it interpolates from known values (at the vertices) across the faces of polygons and computes the appropriate color at all visible points on the surface, at the resolution allowed by the output device (digital file, computer monitor, etc.).
In Data Explorer, we identify connections in the following way. List the sample point location vertices in any order: that list is called the "positions" as we discussed above. Consider each point in the positions list to have an ordinal number, starting at 0 for the first point in the list (these ordinal numbers are not explicitly listed in a Data Explorer file). A connection is denoted by a "list of lists" of numbers in which each entry represents the ordinal values of the points that are to be connected, listed in the order they are to be connected. So for example, if the first point in the positions list is "0.0 0.0" and the second point is "1.0 0.0", we denote a line connection between these two points by "0 1", indicating that a line joins point 0 (first point in the positions list) to point 1 (the second point in the list).
As mentioned above, a triangle connection must reference three positions and a quad references four positions. For complete examples of position and connection lists, see Chapter 3. "Understanding the Data Model".
As a direct extension of this concept, when we define volumetric elements like cubes and tetrahedra, we can perform 3-dimensional interpolation and derive a reasonable data value for any point in a sample volume. The good news about all of this interpolation is that Data Explorer already knows how to do the necessary calculations. As a researcher, your job is to define your data space to Data Explorer--its positions, connections, and data-dependency--but you do not have to worry about the details of how the interpolation is actually performed.
The connections list is optional if it makes no sense to connect your sample points; for example, if you are studying gas molecules, there may be no meaningful interconnecting lines between separate molecules. Nevertheless, you may wish to define "line" connections linking the atoms within each molecule, in order to visualize interatomic bonds or protein backbones; or you may define cubic volumetric elements in the space around the nucleus if you wish to visualize electronic potential fields, for instance.
In any case, you must define a set of connections before you can perform interpolation operations between sampled data values. This is true both for position-dependent data and for connection-dependent data. Once again, positions are discrete points in space, and connections are logical paths between those points representing reasonable interpolation paths between the sampled data values. If you do not have connection information available, you can use the Connect or Regrid modules to create connections for scattered point data.
If you work with regular grids, the "connections" can be defined in a simple way by Data Explorer regardless of the import format you are using. See Chapter 3. "Understanding the Data Model" in this Guide and Chapter 5. "Importing Data" in IBM Visualization Data Explorer QuickStart Guide.
If your work requires irregular grids, you will need to carefully read the section of this manual that describes the format of Data Explorer element types. You may need to write a filter program to convert the connection list output from your finite element program to the format required by Data Explorer before you can import and visualize data sampled on arbitrary structures.
Sometimes in the process of collecting or analyzing data, certain regions or positions have no data value associated with them. For example, an instrument may have a "data drop-out" or a simulation may (for whatever reason) produce an invalid entry. Of course, if you are explicitly listing your positions or connections, you can simply leave those positions out when you create your data file. However, if you have a regular grid (for which you simply list the origin of the grid and the delta in each dimension), this is not convenient. Data Explorer has a way to easily handle this situation, using "invalid positions" and "invalid connections" components. These components are discussed in Chapter 3. "Understanding the Data Model", but briefly, when present in a Field, they instruct any module processing that Field to completely ignore any position or connection identified in that component. For example, an "invalid positions" component may list the integers 0, 15, and 23. This instructs Data Explorer to ignore the positions 0, 15, and 23 (and the data associated with those positions).
You can create these components in a Data Explorer format file (see Appendix B. "Importing Data: File Formats") or, often more easily, using the Include module. For example, suppose in your data file drop-outs are indicated with a data value of 9999, while all valid data lies in the range 0-100. Then set the max parameter of Include to 9998. Include will then remove or invalidate all of the positions with the value 9999. Note that it is usually preferable to set the cull flag of Include to 0 so that the data values are invalidated rather than actually removed (see Include in IBM Visualization Data Explorer User's Reference).
All Data Explorer modules know to ignore invalid data. For example, Streamlines will stop when they reach an invalid element, and Statistics will ignore data values associated with invalid elements.
Given the sets of numbers, "positions," "connections," and "data", we can define a Field, as it is called in Data Explorer. The positions identify locations in space, the (optional) connections define logical continuities (interpolation paths) between positions, and the data are the values measured either at each position or within each connection element. Data Explorer calls each of these sets of numbers (positions, connections, data) a Field component. Components are represented as arrays of numbers with some auxiliary information specifying attributes (e.g., type of dependency). In addition, there are many other types of Field components. The Field is the basic unit of information in Data Explorer, so it is important to understand how to express your data in these terms.
A Field can only have one "positions" and one "connections" component. A Field can have only one component actually named "data", but you may assign names of your choosing to additional components representing other data sets that are also mapped to the same grid. So you can name a "data" component "temperature" and another "wind velocity", or you can just use the default name "data" if you only have one "data" component.
The ".dx" file format provides the most flexibility for describing data sets to Data Explorer. But many researchers produce fairly straightforward arrays of numbers mapped onto regular or deformed regular grids. If your data are already written out in such a form, you may not need to convert your data files into the native ".dx" file format. Instead, Data Explorer's General Array Importer can read your data directly, given a small "header" file that you create to tell the General Array Importer the name of your data file and its dimensions (see Chapter 5. "Importing Data" in IBM Visualization Data Explorer QuickStart Guide).
This shorthand description is enough for Data Explorer to convert your data structure into a Field when it reads your raw data file. You will still find it valuable to understand the components of a Field, because once you begin using the Data Explorer visual programming language, you will have direct access to these components. Much of the power and flexibility of the visual programming language is derived from our ability to access and manipulate Field components in a variety of ways.
[ OpenDX Home at IBM | OpenDX.org ]