- a)
- Siirtymätodennäköisyyksien
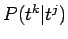 suurimman uskottavuuden
estimaatti on
suurimman uskottavuuden
estimaatti on
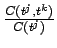 . Siis esimerkiksi
todennäköisyys
. Siis esimerkiksi
todennäköisyys
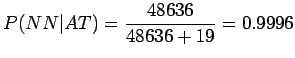
Kun parametrien määrä on pieni ja dataa on paljon, suurimman uskottavuuden estimaatit ovat riittävän hyvät. Taulukkoon 1 on laskettu siirtymätodennäköisyys kaikkin sanaluokkien välille.
Havaintotodennäköisyyksien
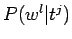 suurimman uskottavuuden
estimaattori on
suurimman uskottavuuden
estimaattori on
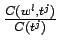 . Eli esimerkiksi
todennäköisyys sille, että VB-tilassa olessa havaitaan sana bear
on
. Eli esimerkiksi
todennäköisyys sille, että VB-tilassa olessa havaitaan sana bear
on
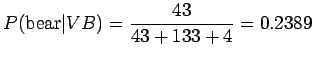
Taulukkoon 2 on merkitty pyydetyt havaintotodennäköisyydet.
Taulukko: Havaintotodennäköisyydet AT BEZ IN NN VB PISTE bear 0 0 0 0.0187 0.2389 0 is 0 1 0 0 0 0 move 0 0 0 0.0672 0.7389 0 on 0 0 1 0 0 0 president 0 0 0 0.7127 0 0 progress 0 0 0 0.2015 0.0222 0 the 1 0 0 0 0 0 . 0 0 0 0 0 1
- b)
- Tehtävässä pyydettiin laskemaan tilojen
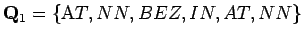 ja
ja
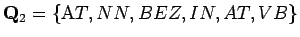 todennäköisyyksien suhde kun
tiedetään havainnot
todennäköisyyksien suhde kun
tiedetään havainnot
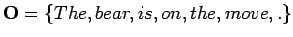 . Merkitään juuri laskettuja mallin parametreja
. Merkitään juuri laskettuja mallin parametreja 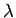 :lla.
:lla.
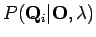
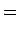
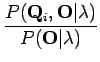
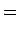
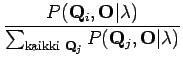
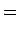
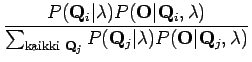
Yhtälöä on pyöritetty perustodennäköisyyskaavojen avulla. Huomataan, että yhtälön yläpuoli on helppo laskea: Tiedämme tilasekvenssin, joten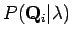 ei tuota
vaikeuksia kuten ei myöskään
ei tuota
vaikeuksia kuten ei myöskään
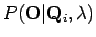 . Nimittäjän normalisointitermi on hankalampi, meidän
pitäisi siis laskea yhteen kaikkien mahdollisten tilasekvenssejen
todennäköisyydet kun tiedämme havainnot. Tämä voitaisiin laskea
tehokkaasti eteenpäin-algoritmilla (katso edellinen
laskari). Normalisointitermi on kuitenkin vakio kaikille
sekvensseille ja koska kysymyksessä pyydettiin vain kahden sekvenssin
todennäköisyyksien suhdetta, meidän ei tässä tarvitse siis
ratkaista vakion arvoa ollenkaan.
. Nimittäjän normalisointitermi on hankalampi, meidän
pitäisi siis laskea yhteen kaikkien mahdollisten tilasekvenssejen
todennäköisyydet kun tiedämme havainnot. Tämä voitaisiin laskea
tehokkaasti eteenpäin-algoritmilla (katso edellinen
laskari). Normalisointitermi on kuitenkin vakio kaikille
sekvensseille ja koska kysymyksessä pyydettiin vain kahden sekvenssin
todennäköisyyksien suhdetta, meidän ei tässä tarvitse siis
ratkaista vakion arvoa ollenkaan.
Ratkaistaan todennäköisyyksien suhde:
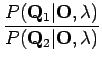
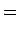
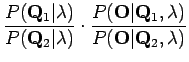
Ratkaistaan ensin ensimmäinen termi:
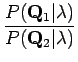
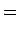
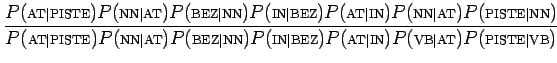
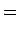
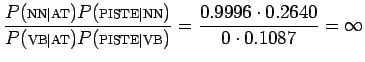
Huomataan, että pelkästään siirtymätodennäköisyyksiä katselemalla sanaluokkasekvenssi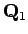 on äärettömän paljon
todennäköisempi.
on äärettömän paljon
todennäköisempi.
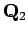 :den todennäköisyyshän on nolla.
:den todennäköisyyshän on nolla.
Katsellaan vielä havaintotodennäköisyyksiä, ettei sieltä tule mitään yllätyksiä sekoittamaan edellisen kohdan perusteella tehtyjä päätelmiä:
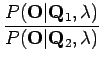
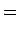
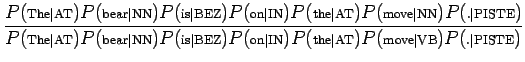
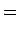
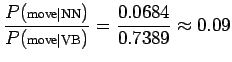
Koska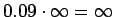 , mallimme mukaan on äärettömän
paljon todennäköisempää, että sana move on nomini
(NN) tässä lausessa.
, mallimme mukaan on äärettömän
paljon todennäköisempää, että sana move on nomini
(NN) tässä lausessa.
- c)
- Viterbi-haku on tarkemmin käsitelty edellisessä
laskarissa. Alustetaan algorimi niin, että lähtötila on edellisen
lauseen lopetuspiste:
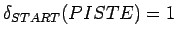 ja
ja
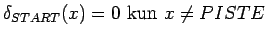 .
.
Lasketaan tässä esimerkiksi muutaman tilan arvo. Koska sana the voi tulla vain tilasta AT (koska
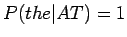 ja
ja
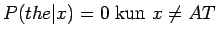 ), täytyy
ensimmäisen tilan siis olla AT. Siihen kertyvä todennäköisyys on
), täytyy
ensimmäisen tilan siis olla AT. Siihen kertyvä todennäköisyys on
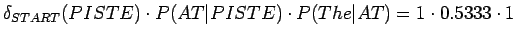 .
.
Sana bear voi tulla tiloista NN tai VB, mutta tilasta AT voidaan siirty vain tilaan NN. Seuraavan tilan täytyy siis olla NN. Siihen on kertynyt todennäköisyyttä
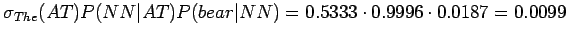 .
.
Samalla tavalla jatkamalla huomataan, että on ainoastaan yksi polku, joka johtaa alusta loppuun. Muissa kohdissa joko havaintomatriisin tai siirtymämatriisin nollat katkaisevat reitin. Paras polku on piirretty kuvaan 1. Siitä voidaan lukea, että paras tilasekvenssi
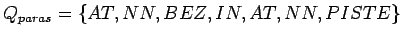 .
.
Kuva: Viterbi-haku. Matriisien harvuuden vuoksi (paljon nollia) ei hilaan tule juurikaan yli nollatodennäköisyydellä tapahtuvia siirtymiä. Siirtymiä, joiden todennäköisyys on nolla, ei ole piirretty. 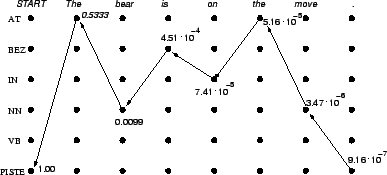
- box: VB
 NN
NN
- board: VB
 NN
NN
- crash: VB
 NN
NN
Seuraava sääntö sopii vain toiseen lauseeseen. Muutetaan
- marked: VBD
 VBN
VBN
Kolmas sääntö sopii vain jos sana wanted on luokiteltu
![]() :ksi ja sitä seuraa TO. Tämä sopii ensimmäiseen lauseeseen ja
muutetaan siis
:ksi ja sitä seuraa TO. Tämä sopii ensimmäiseen lauseeseen ja
muutetaan siis
- wanted: RB
 VBD
VBD
Viimeinen sääntö sopii vain ensimmäiseen lauseeseen:
- look: NN
 VB
VB
Korjatut lauseet ovat siis:
- I)
PN VBD TO VB IN AT NN I wanted to look inside the box - II)
PN BEZ RB VBN IN AT NN It was clearly marked on the board - III)
AT NN PN BEZ AT VB NN The plane he is on will crash