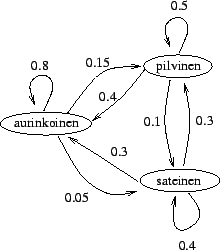
- a)
- Kuvaan 1 on piirretty Turun säätila Markov-ketjuna.
- b)
- Lasketaan tilasekvenssin
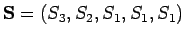 todennäköisyys kun tiedetään, että lähdetään tilasta
todennäköisyys kun tiedetään, että lähdetään tilasta 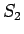 . Haluamme
siis laskea todennäköisyyttä
. Haluamme
siis laskea todennäköisyyttä
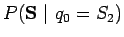
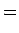
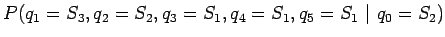
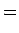
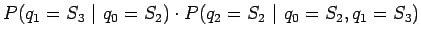
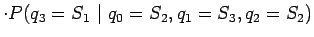
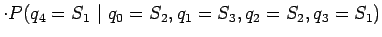
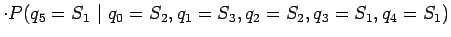
Sovelletaan ylläolevaan kaavaan Markov-oletusta, että nykyinen tila
riippuu vain edellisestä tilasta, muttei sitä aikaisemmista:
Tämä vastaa taulukoituja kertoimia
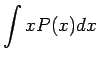 |
|||
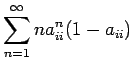 |
|||
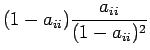 |
|||
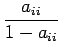 |
Aurinkoisen päivän tapauksessa
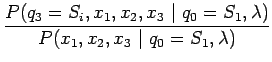 |
|||
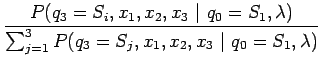 |
Ylläolevan yhtälön pyörittämiseen käytettiin ensiksi
todennäköisyyslaskun kaavaa
![]() . Sitten huomattiin että
. Sitten huomattiin että
![]() . Edellisen yhtällön nimittäjässä ja
osoittajassa on samankaltainen termi. Kevennetään hieman merkintöjä
ja esitetään sama asia funktion
. Edellisen yhtällön nimittäjässä ja
osoittajassa on samankaltainen termi. Kevennetään hieman merkintöjä
ja esitetään sama asia funktion
![]() avulla:
avulla:
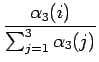 |
Tarkastellaanpa, miten tämä eteenpäin-todennäköisyys
![]() oikein voidaan laskea.
oikein voidaan laskea.
Lähtöpäivä


Ensimmäinen päivä

 Toinen päivä
Toinen päivä

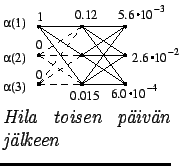
Kolmas päivä
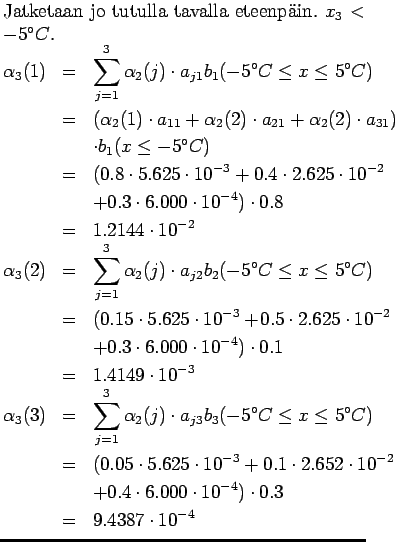
Nyt olemme saaneet lasketuksi tehtävän ratkaisuun tarvittavat suureet.
Sijoitetaan luvut kaavaan:
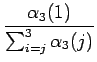 |
|||
 |
|||
Palatessa on siis 89 % todennäköisyydellä aurinkoista. Samalla tavalla voidaan laskea pilvisen sään todennäköisyys 10 % ja sateisen sään todennäköisyys 1 %.
b) Halusimme vielä arvata, mikä oli todennäköisin sääsekvenssi poissa ollessamme. Tämän voimme hoitaa Viterbi-algoritmilla, joka on hyvin samankaltainen eteenpäin-algoritmin kanssa. Nyt vain joka tilassa lasketaan todennäköisyys parhaan reitin kautta sen sijaan että summattaisiin kaikkien reittejen yli. Viterbi: Lähtöpäivä


Viterbi: Ensimmäinen päivä

 Viterbi: Toinen päivä
Viterbi: Toinen päivä

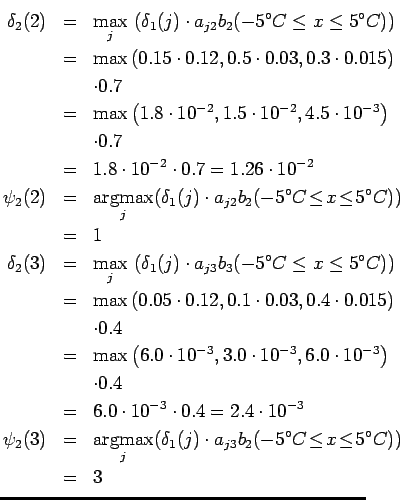
 Laskettaessa
Laskettaessa ![]() huomataan, että
kahdesta paikkaa (tilat 1 ja 3) päästään yhtä todennäköisesti tilaan 3. Tässä
tapauksessa paras paluureitti ratkaistiin arpomalla näiden kahden
välillä ja tulokseksi saatiin 3.
huomataan, että
kahdesta paikkaa (tilat 1 ja 3) päästään yhtä todennäköisesti tilaan 3. Tässä
tapauksessa paras paluureitti ratkaistiin arpomalla näiden kahden
välillä ja tulokseksi saatiin 3.
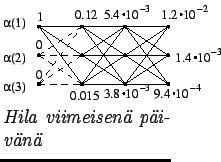
Viterbi: Kolmas päivä

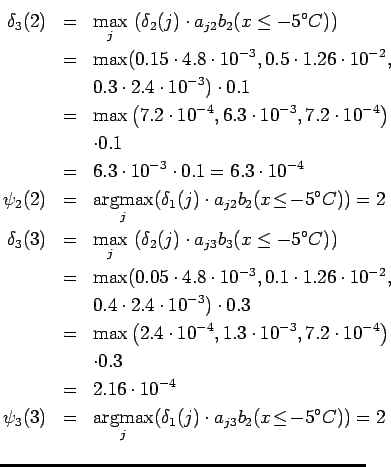
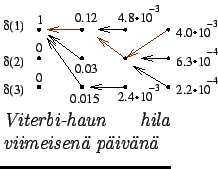 Valmiista hilasta voidaan hakea todennäköisin tilasekvenssi:
aloitetaan kaikkein todennäköisimmästä lopputilasta ja seurataan
nuolia alkuun päin. Nyt siis näyttäisi siltä, että aurinkoisen
lähtöpäivän jälkeen Turussa on ollut aurinkoista, pilvistä ja taasen
aurinkoista.
Valmiista hilasta voidaan hakea todennäköisin tilasekvenssi:
aloitetaan kaikkein todennäköisimmästä lopputilasta ja seurataan
nuolia alkuun päin. Nyt siis näyttäisi siltä, että aurinkoisen
lähtöpäivän jälkeen Turussa on ollut aurinkoista, pilvistä ja taasen
aurinkoista.
Yhteenveto: mitä eroa eteenpäin-algoritmilla ja Viterbi-haulla
Eteenpäin-algoritmi hakee oikean todennäköisyyden kullekin tilasekvenssille. Sen avulla ei kuitenkaan pysty hakemaan parasta polkua hilasta.
Viterbi-haulla tilatodennäköisyydet ovat vain approksimaatioita. Tätä algorimia kuitenkin käytetään paljon juuri sen takia, että sillä pysytytään löytämään paras polku.
Laskennallisesti algoritmit ovat yhtä raskaita, eteenpäin-algoritmin summaus on vain Viterbi-haussa vaihtunut maksimoinniksi.