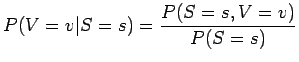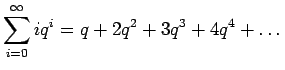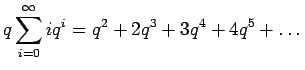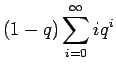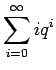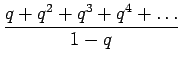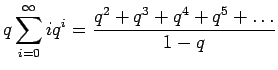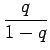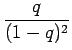- a)
- Sijoitetaan entropian kaavaan
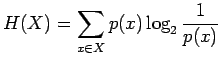
tehtävässä annetut arvot:
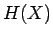

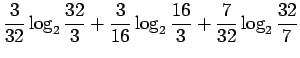
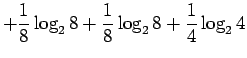

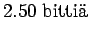
- b)
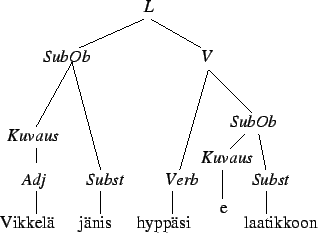
- Tehtävän ratkaisuun tarvitaan todennäköisyyttä
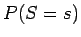 (eli satunnainen
substantiivi on
(eli satunnainen
substantiivi on 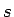 ). Tämä todennäköisyys saadaan tehtävänannon
taulukon oikeasta marginaalista. Lisäksi tarvitaa todennäköisyyttä
). Tämä todennäköisyys saadaan tehtävänannon
taulukon oikeasta marginaalista. Lisäksi tarvitaa todennäköisyyttä
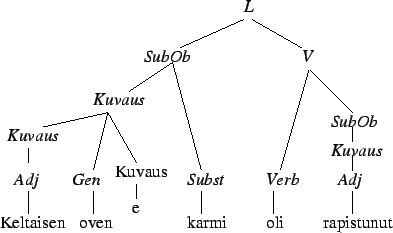
Lähteen entropia, kun tiedetään, että edellinen symboli kuului joukkoon
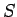 on
on
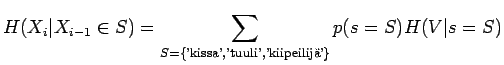
Tämän laskemiseksi meidän pitää osata laskea ehdollinen entropia
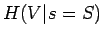 . Lasketaan tämä sanalle 'kissa':
. Lasketaan tämä sanalle 'kissa':
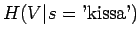

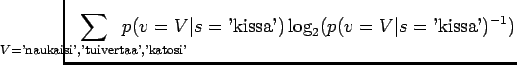

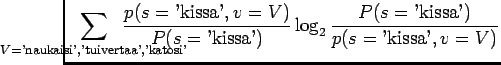

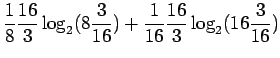

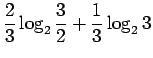
Kun sijoitamme jokaista joukon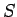 sanaa vastaavat todennäköisyydet, saamme
sanaa vastaavat todennäköisyydet, saamme
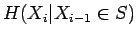

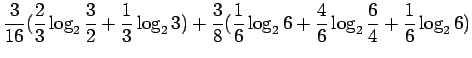
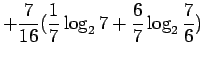

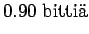
Mikä on sitten todennäköisyys, että satunnainen sana on 'kissa' ?
Koska molemmat luokat ![]() ja
ja ![]() ovat yhtä todennäköiset, tulos on
ovat yhtä todennäköiset, tulos on
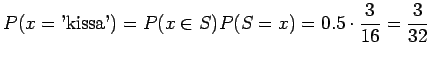 |
Huomaamme, että a)-kohta on itseasiassa b)-kohdan marginaalijakauma.
Tästä voimme päätellä, että kun tunnemme lähteen toiminnan paremmin, sen tuottamat sanat ovat vähemmän yllättäviä ja voimme koodata ne vähemmällä määrällä bittejä (0.9 bittiä < 2.5 bittiä).
- a)
- Kunkin alkeistapauksen todennäköisyys on
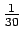 . Alkeistapauksia on 30. Sijoitetaan entropian kaavaan:
. Alkeistapauksia on 30. Sijoitetaan entropian kaavaan:
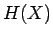

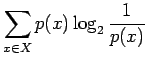

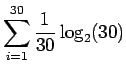

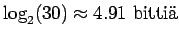
- b)
- Sanan, jossa on vain yksi merkki, sanotaan vaikka joukon
ensimmäinen merkki, todennäköisyys on
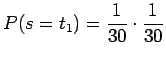
sillä ensimmäisen merkin pitää olla joukon ensimmäinen ja sitten pitää tulla sanaväli. Tällaisia sanoja on 29 kappaletta.Vastaavasti, tietyn kahden merkin pituisen sanan todennäköisyys on
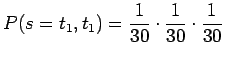
Tällaisia sanoja on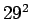 kappaletta. Homma jatkuu samalla tavalla
useammille sanoille.
kappaletta. Homma jatkuu samalla tavalla
useammille sanoille.
Lasketaan tällaisen lähteen entropia:
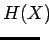

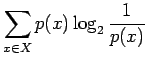


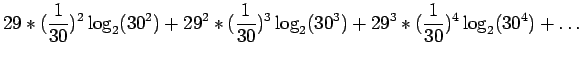


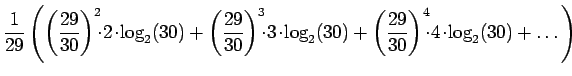


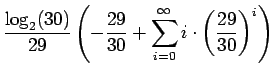
Kerrotaan yhtälö
Vähennetään yhtälö 2 puolittain yhtälöstä 1
Kerrotaan yhtälö 4 vielä kerran
Nyt vähennetään yhtälöt 4 ja 5 toisistaan ja saadaan ratkaisu:
Tässä ratkaisussa pitää vielä huomioda, että jotta yhtälö 2 voidaan vähentää yhtälöstä 1, pitää sarjojen olla suppenevia, eli
Kun tämä hässäkkä sijoitetaan alkuperäiseen ongelmaan, saadaan
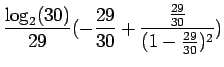 |
|||
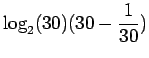 |
|||
Ensi silmäyksellä tämä tulos saattaa tuntua hämmentävältä, eikä tuloksen pitäis olla sama kuin a)-kohdassa ? Pikainen tarkistuslasku ehkä hälventää hieman epäluuloja: Sanan pituuden oletusarvo on 29, eli entropia per merkki on n.
On myös syy, miksi tulosten ei pitäisi olla aivan samat: Ensimmäinen lähde voi tuottaa sanan, jossa on kaksi välilyöntiä peräkkäin, kun taas toinen lähde ei voi annetun formuloinnin mukaan sitä tuottaa. Tästä johtuen pitäisi toisen lähteen entropia per merkki olla hieman alempi.
- a)
- Merkitään mallin yksi antamaa hämmentyneisyyttä
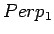 , mallin 2
puolestaan
, mallin 2
puolestaan 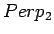 ja niin edelleen.
ja niin edelleen.
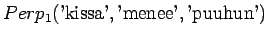
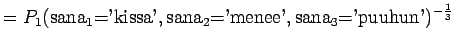
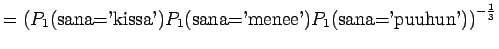
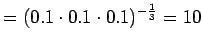
Malli 1 siis valitsee koko ajan keskimäärin kymmenestä eri sanasta. Tulos vaikuttaa oikealta. Entäpä malli 2 ?
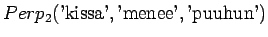

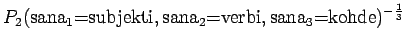

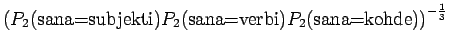

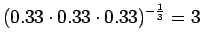
Malli 2 valitsee keskimäärin 3:sta eri vaihtoehdosta, tulos vaikuttaa järkevältä.
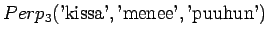

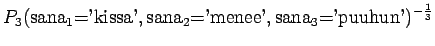

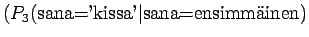
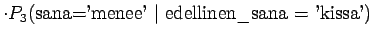
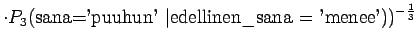

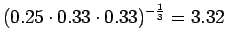
Tämä malli valitsee siis keskimäärin 3.32 sanasta koko ajan.Tämän esimerkin valossa kielimallit 1 ja 3 ovat vertailukelpoiset. Kielimalli 3 vaikuttaa näistä selvästi paremmalta. Kielimalli 2 ei voi verrata muihin, sillä se operoi selvästi pienemmällä symbolijoukolla. Selvempi esimerkki olisi ehkä kielimalli, jonka mielestä kaikki sanat kuuluvat ryhmään 1 ja tämän ryhmän todennäköisyys on siis 1. Tämä kielimalli siis hämmentyneisyyden mukaan täydellinen, sillä se ei ole yhtään yllättynyt mistään sanasta.
- b)
- Tarkastellaanpa vielä toista testilausetta. Mallille 1
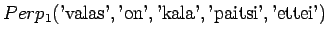

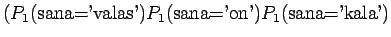
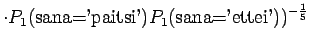

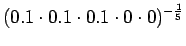

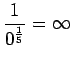
Huomataan, ettei hämmentyneisyyttä voida laskea, jos malli asettaa testijoukon sanalle todennäköisyyden nolla. Usein nämä sanat jätetään huomiotta ja saadaan siis
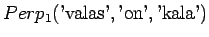

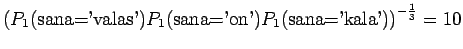
Jotta tulos olisi mielekäs, on nyt myös ilmoitettava ohi kieliopin menneet sanat, tässä tapauksessa siis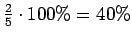 sanoista ei
osunut kielioppiin. Mallille 2 sadaan vastaavasti
sanoista ei
osunut kielioppiin. Mallille 2 sadaan vastaavasti
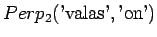

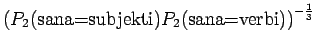

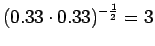
Ohi kieliopin menee myös 60% sanoista.Malliin kolme sopii vain kaksi ensimmäistä sanaa:
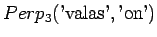

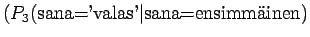
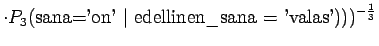

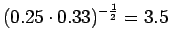
Tässä siis 60% sanoista menee ohi kieliopin.Ovatko b)-kohdan tulokset vertailukelpoisia ? Malli 2 voidaan diskata samoilla perusteilla kuin a)-kohdassakin. Malleja 1 ja 3 voidaan vertailla, kun otetaan myös huomioon ohi kieliopin menneet sanat. Malli 1 kattaa sanaston paremmin, mutta malli 3 antaa paremman hämmentyneisyyden. Usein kielimallin laatiminen on tasapainottelua näiden kahden ominaisuuden välillä.