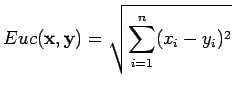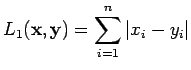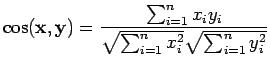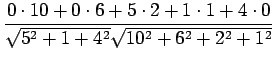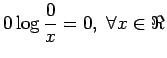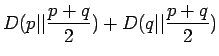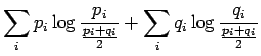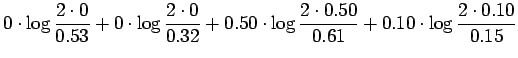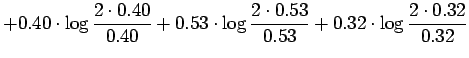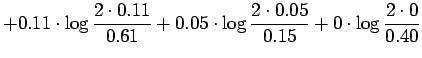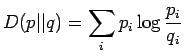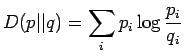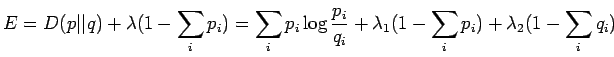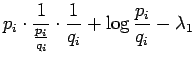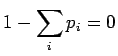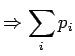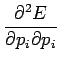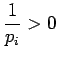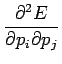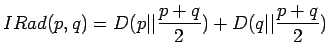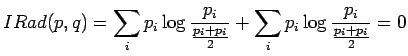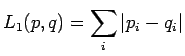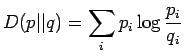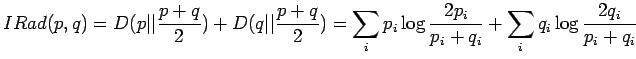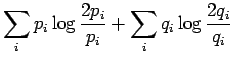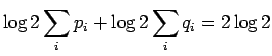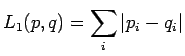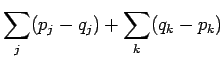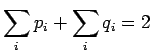T-61.281 Luonnollisten kielten tilastollinen käsittely
Vastaukset 9, ti 25.3.2003, 16:15-18:00 Samankaltaisuusmitat, Versio 1.1
- 1.
-
Euklidinen etäisyys vektorin
![$ \mathbf x =[x_1 ~x_2 \dots x_n]$](img2.gif) ja
ja
![$ \mathbf y =[y_1 ~y_2 \dots y_n]$](img3.gif) välillä määritellään
välillä määritellään
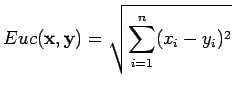 |
(1) |
Lasketaan euklidinen etäisyys esimerkin vuoksi Tintuksen ja
Korvalääkkeen välillä:
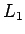 -normin mukainen etäisyys määritellään
-normin mukainen etäisyys määritellään
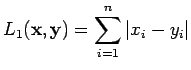 |
(2) |
Lasketaan etäisyydet:
Kosini onkin sitten hieman erilainen tapaus, se on
samankaltaisuusmitta. Se määritellään vaikkapa
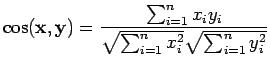 |
(3) |
Lasketaan etäisyydet:
Tässä siis suurempi luku vastaa suurempaa samankaltaisuutta ja
etäisyydet / samankaltaisuudet ovat samassa järjestyksessä kuin edelläkin.
Informaatiosäteen laskemista varten muodostetaan suurimman
uskottavuuden estimaatit sille, että seuraava lähteen 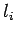 (Tintus,
Korvalääke, Termiitti) tuottama tunnettu sana on
(Tintus,
Korvalääke, Termiitti) tuottama tunnettu sana on 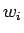 . Tämä voidaan
laskea jakamalla jokainen annetun matriisin rivin alkio rivin
alkioiden summalla (Taulukko 1).
. Tämä voidaan
laskea jakamalla jokainen annetun matriisin rivin alkio rivin
alkioiden summalla (Taulukko 1).
Taulukko:
ML-estimaatti sanatodennäköisyyksille
| |
raikas |
hapokas |
makea |
hedelmäinen |
pehmeä |
| Tintus |
0 |
0 |
0.50 |
0.10 |
0.40 |
| Korvalääke |
0.53 |
0.32 |
0.11 |
0.05 |
0 |
| Termiitti |
0.07 |
0.29 |
0.21 |
0.21 |
0.21 |
|
Määritellään vielä, että
Informaatiosäde voidaan laskea kaavasta
Lasketaan informaatiosäde annetuille lähteillä:
Huomataan, että kaikki mitat asettavat lääkeet asettavat lääkkeet
samankaltaisuuksin mukaan samaan järjestykseen: Tintus ja Termiitti
ovat samankaltaisimmat, Tintus ja Korvalääke erilaisimmat.
KL-divergenssin määritelmästä voimme suoraan nähdä muutaman siihen
liittyvän ongelman:
KL-divergenssi ei ole symmetrinen, vaan pitäisi aina päättää kumpi
lääke on referenssilääke, mihin toista verrataan. Toinen ongelma on
siinä, että jos referenssilääkkeellä on nollatodennäköisyys jossain,
missä vertailtava lääke ei ole nolla, niin KL-divergenssi menee
äärettömyyksiin.
[2.]
KL-divergenssin määritelmä on
Etsitään jakauma, joka minimoi KL-divergenssin. Lisätään
Lagrange-kerroin 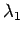 pitämään huolta siitä, että
pitämään huolta siitä, että 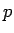 pysyy
todennäköisyysjakaumana (eli
pysyy
todennäköisyysjakaumana (eli
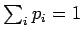 ) ja
) ja 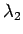
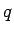 :lle.
:lle.
Merkitään osittaisderivaatta 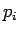 :n suhteen nollaksi:
:n suhteen nollaksi:
Ratkaistaan 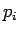 :
:
Lasketaan osittaisderivaatta 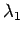 suhteen:
suhteen:
Samanlainen tulos saadaan 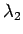 :lle ja
:lle ja 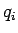 :lle.
Osittaisderivaattojen nollakohdista voimme päätellä että
:lle.
Osittaisderivaattojen nollakohdista voimme päätellä että
Toisen asteen derivaattoja tarkastelemalla voimme vielä varmistua
siitä että tämä todellakin on minimi eikä maksimi:
Jos sijoitamme KL-divergenssin
kaavaan 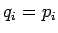 saamme divergenssiksi nolla. Eli
KL-divergenssi on nolla jos ja vain jos jakaumat
saamme divergenssiksi nolla. Eli
KL-divergenssi on nolla jos ja vain jos jakaumat 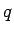 ja
ja 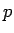 ovat samoja.
ovat samoja.
Informaatiosäteen määritelmä on
Laskimme juuri, että KL-divergenssi on nolla, kun jakaumat ovat samat
ja muuten tätä enemmän. Informaatiosäteen tapauksessa
nolladivergenssiin siis päästään myös vain kun 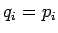 :
:
Ehto on siis sama kuin KL-divergenssillä
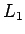 -normin määritelmä on
-normin määritelmä on
Tämähän on selvästi pienimmillään nolla. Se tapahtuu kun 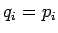 .
.
Huomataan siis, että kaikki mitat antavat nollaetäisyyden samalla
ehdolla: jakaumien on oltava samat.
[3.]
Katsotaan vielä KL-divergenssin määritelmää:
Huomataan, että jos 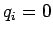 kun
kun 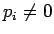 , saadaan etäisyydeksi
, saadaan etäisyydeksi
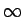 .
.
Kirjoitetaan informaatiosäteen määritelmä auki:
Intuition avulla arvataan sopivaksi jakaumaksi sellainen, missä
jakaumat sijaitsevat täysin eri alueilla:
Sijoitetaan tällaiset jakaumat informaatiosäteen lausekkeeseen:
Huomataan, että ehdot täyttävä jakauma antaa suurimman
etäisyyden. Todistus siitä, että 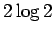 on suurin mahdollinen
informaatiosäde ja että ylläarvatut ehdot vaaditaan tämän etäisyyden
saavuttamiseksi olisi sitten jonkin verran hankalampi.
on suurin mahdollinen
informaatiosäde ja että ylläarvatut ehdot vaaditaan tämän etäisyyden
saavuttamiseksi olisi sitten jonkin verran hankalampi.
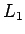 -normin määritelmähän oli
-normin määritelmähän oli
Intuitiollahan voisi jo päätellä, että vastaus on sama kuin
informaatiosäteen tapauksessa, mutta yritetään perustella asiaa vielä
matemaattisesti. Jaetaan alkeistapaukset 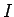 kahteen osaan. Osassa
kahteen osaan. Osassa 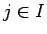 on tapaukset, joissa
on tapaukset, joissa 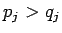 ja osassa
ja osassa 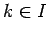 tapaukset,
joissa
tapaukset,
joissa 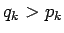 . Kirjoitetaan itseisarvot auki:
. Kirjoitetaan itseisarvot auki:
Koska todennäköisyydet ovat positiivissa ja summautuvat 1:een, suurin
etäisyys saadaan kun
eli etäisyys on
Informaatiosäteen ja 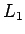 -normin tapauksessa suurimman etäisyyden
saavuttamiseen vaaditaan samat ehdot. Sen sijaan KL-divergenssi menee
äärettömyyksiin jo, kun vertailujakauma
-normin tapauksessa suurimman etäisyyden
saavuttamiseen vaaditaan samat ehdot. Sen sijaan KL-divergenssi menee
äärettömyyksiin jo, kun vertailujakauma 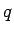 on nolla jossain missä
on nolla jossain missä 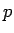 ei ole nolla.
ei ole nolla.
vsiivola@cis.hut.fi