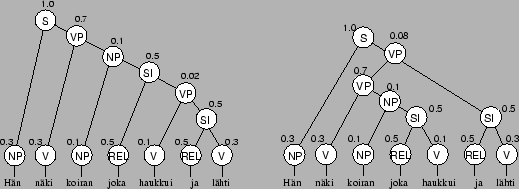
Nyt voimmekin laskea kummankin jäsennyksen todennäköisyydet
kertomalla kaikki kuvasta löytyvät todennäköisyydet
Huomataan, että mallin mukaan toinen jäsennys on todennäköisempi. Ilman muuta tietoa tai oikein pilkutettua tekstiä lienee mahdotonta päätellä, kumpi jäsennys on oikea.
Merkitään
![]() todennäköisyyttä, että puulla, joka kattaa
sanat
todennäköisyyttä, että puulla, joka kattaa
sanat ![]() :stä
:stä ![]() :hen on juurena jäsennys
:hen on juurena jäsennys ![]() . Nyt siis voimme
alustaa algoritmin
. Nyt siis voimme
alustaa algoritmin
![]() arvot lehdille. Koska suurin osa lauseen
sanoista voi olla kotoisin vain yhdestä ei-terminaalisymbolista,
alustus on helppoa:
arvot lehdille. Koska suurin osa lauseen
sanoista voi olla kotoisin vain yhdestä ei-terminaalisymbolista,
alustus on helppoa:

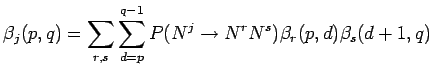 |
Tässä siis summataan kaikkien mahdollisten sääntöjen (
Lasketaanpa sitten seuraavat arvot. Nyt kukin alipuulla koostuu kahdesta lapsesta ja juuresta:
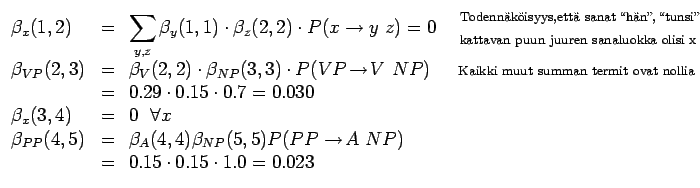
Koskapa kieliopissa yhdellä solmulla olla vain kaksi lasta, saadaan seuraavalle kierrokselle todennäköisyydet summaamalla:
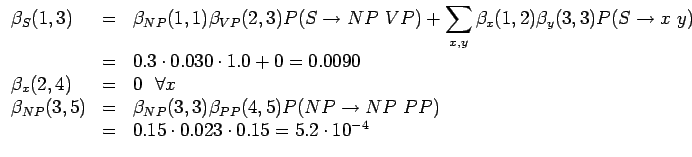
Vielä on pari kierrosta jäljellä:
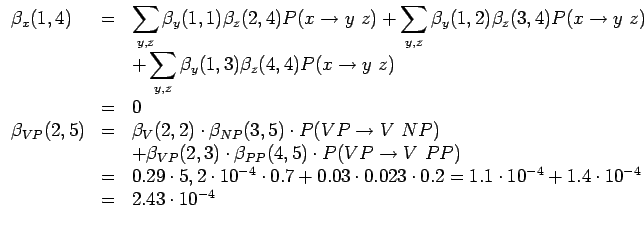
Lasketaanpa vielä homma loppuun ennen tarkempia pohdintoja.
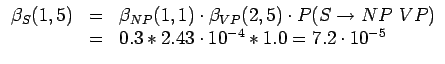
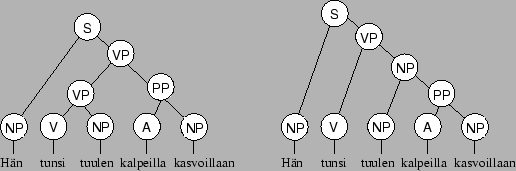
Kuvaan 2 on piirretty mahdolliset jäsennykset. Mallin mukaan hieman todennäköisempi jäsennys on väärä, johtunee siitä että alkuperäinen malli oli hihasta ravistettu.
Oletetaan, että sarja konvergoi johonkin arvoon (todistetaan
myöhemmin). Tällaisessa tilanteessa
![]() eli
eli
| 0 | |||
| 0 |
Viimeisellä rivillä on
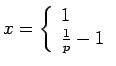
| 0 | |||
| 0 |
Toisen asteen yhtälön ratkaisukaavan avulla saadaan, että funktio on kasvava jos:
Näistä toinen alue on relevantti meille. Osoitetaan vielä, että funktio kasvaa asymptoottisesti kohti pienempää juurta
Eli sarja voi saada yhtä suurempia arvoja vain, jos sarjan edellinen arvo oli jo suurempi kuin yksi. Nyt lähdemme liikkeelle nollasta
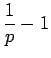 |
|||
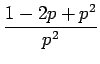 |
|||
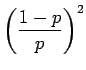 |
Saadaan ehdot
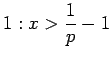 |
|||
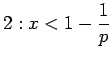 |
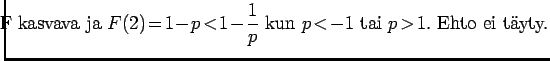 |
Myöskään tämän juuren ohi ei voi päästä. Sarjan summa on siis
Jos olisi ovelampi matemaatikko, tehtävän pystyisi ratkaisemaan muutamalla rivillä. Tarkastelemalla mallin generoimien ei-terminaalien määrän oletusarvoa verrattuna mallin generoimien terminaalien määrän oletusarvoon, päätynee samaan tulokseen.