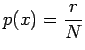T-61.281 Luonnollisten kielten tilastollinen käsittely
Vastaukset 5, ti 25.2.2003, 16:15-18:00 N-grammikielimallit, Versio 1.0

1.
Alla on erään henkilön ja tilaston estimaatit sille, miten todennäköistä on, että alla annetut sanat seuraavat sanoja ``tuntumaan jo'':

Taulukko: Ihminen vs tilasto, trigrammiestimaatit
sana tilasto trig ihminen trig ihminen lause
ja 0.00 0.00 0.00
hyvältä 1.00 0.18 0.40
kumisaapas 0.00 0.00 0.00
keväältä 0.00 0.23 0.50
ilman 0.00 0.05 0.05
päihtyneeltä 0.00 0.20 0.00
turhalta 0.00 0.23 0.05
koirineen 0.00 0.00 0.00
öljyiseltä 0.00 0.11 0.00
Turku 0.00 0.00 0.00


Tarkemmalla tukimisilla huomataan, että taulukossa ihmisen antamat trigrammiestimaatit ovat jonkin verran pielessä ja tilastolliset pehmentämättömät trigrammiestimaatit aivan pielessä.

Tilastollisten estimaattien laskuun käytettiin n. 30 miljoonan sanan aineistoa. Tässä aineistossa ei yksikään annetuista taivutetuista trigrammeista esiintynyt kertaakaan. Trigrammit perusmuotoistamalla löydettiin 11 lausetta, joissa esiintyi ``tuntua jo hyvä''. Estimaatti kaipaa siis selvästi tasoittamista, eikä senkään jälkeen ole kovin luotettava.

Myös esimerkki-ihmisen antama estimaatti on hieman pielessä, aivan mahdolisesille lauseille on asetettu nollatodennäköisyys, esim. ``Kyllä alkaa tuntumaan jo kumisaapas jalassa'', lause joka voidaan tokaista vaikka pitkän vaelluksen päätteeksi.

Kun testihenkilölle annettiin koko lause nähtäväksi, saatiin jo varsin laadukkaat estimaatit. Jotta tilastollisesti pystyttäisiin pääsemään samaan tulokseen, tarvitsisi mallin ymmärtää suomen kielen syntaksia (miten sanoja voidaan taivuttaa ja laittaa peräkkäin) sekä myös sanojen semanttista merkitystä (``helmikuu'' on lopputalvea, melkein kevättä).

2.
a)
Seuraavalla sivulla on esitetty tekstistä löydetyt n-grammit. Huomataan, että etenkin bi- ja trigrammien kohdalla data on erittän harvaa, juuri mitään yksikköä ei ole huomattu kertaa enempää.

Unigrammit 
alkuperäinen 1
aloittaa 1
alun, 1
antaa 3
arvioida 2
ei 1
erilainen 1
estimaatti 3
helmikuu 1
hyvä 2
ihminen 1
ilma 1
ja 2
jatkosana 1
jo 2
joka 1
jolloin 1
jotta 1
järjestys 1
kannattaa 1
kertyä 1
kevät 1
kielioppiaineisto 1
kielioppimalli 1
kohta 2
koira 1
koko 1
konteksti 1
kumisaapas 1
kumpi 1
kurkkia 1
kuu 1
kääntöpuoli 1
laskea 1
lause 2
leuto 1
löytyä 1
mahdollinen 1
mennä 1
mikä 1
nyt 1
oikea 1
olla 5
paperi 1
peruste 1
pystyä 1
päihtyä 1
saada 1
sana 5
se 2
seuraava 2
soidinmeno 1
suorituskyky 1
sää 1
tarvita 1
tasoittamaton 1
tehdä 1
tehtävä 2
tiainen 1
tieto 2
tietää 1
todennäköisyys 3
tuntumaa 2
turha 1
turku 1
tämä 2
uudestaan 1
vaikuttaa 1
vastata 1
verrata 1
x 1
öljyinen 1
Bigrammit 
alkuperäinen lause 1
aloittaa tiainen 1
alun, joka 1
antaa estimaatti 1
antaa hyvä 1
antaa sana 1
arvioida nyt 1
arvioida sana 1
ei vaikuttaa 1
erilainen tieto 1
estimaatti ei 1
estimaatti kielioppiaineisto 1
estimaatti kumpi 1
helmikuu tuntumaa 1
hyvä kumisaapas 1
hyvä todennäköisyys 1
ihminen suorituskyky 1
ilma päihtyä 1
ja hyvä 1
ja soidinmeno 1
jatkosana olla 1
jo seuraava 1
jo x 1
joka olla 1
jolloin estimaatti 1
jotta se 1
järjestys kurkkia 1
kannattaa tehdä 1
kertyä tieto 1
kevät ilma 1
kielioppiaineisto laskea 1
kielioppimalli tarvita 1
kohta alkuperäinen 1
kohta jolloin 1
koira öljyinen 1
koko lause 1
konteksti peruste 1
kumisaapas kevät 1
kumpi antaa 1
kurkkia seuraava 1
kuu se 1
laskea tasoittamaton 1
lause alun, 1
lause olla 1
leuto sää 1
löytyä paperi 1
mahdollinen jatkosana 1
mennä kertyä 1
mikä erilainen 1
nyt tämä 1
oikea sana 1
olla arvioida 1
olla ja 1
olla leuto 1
olla saada 1
olla sana 1
paperi kääntöpuoli 1
peruste uudestaan 1
pystyä vastata 1
päihtyä turha 1
saada helmikuu 1
sana löytyä 1
sana tietää 1
sana todennäköisyys 2
sana tuntumaa 1
se mennä 1
se pystyä 1
seuraava kohta 1
seuraava sana 1
soidinmeno aloittaa 1
suorituskyky kohta 1
sää ja 1
tarvita jotta 1
tasoittamaton estimaatti 1
tehdä järjestys 1
tehtävä kannattaa 1
tehtävä olla 1
tiainen olla 1
tieto kielioppimalli 1
tieto tehtävä 1
tietää koko 1
todennäköisyys mahdollinen 1
todennäköisyys mikä 1
todennäköisyys oikea 1
tuntumaa jo 2
turha koira 1
turku verrata 1
tämä konteksti 1
tämä tehtävä 1
uudestaan antaa 1
vaikuttaa kuu 1
vastata ihminen 1
verrata antaa 1
x arvioida 1
öljyinen turku 1
Trigrammit 
alkuperäinen lause olla 1
aloittaa tiainen olla 1
alun, joka olla 1
antaa estimaatti kielioppiaineisto 1
antaa hyvä todennäköisyys 1
antaa sana todennäköisyys 1
arvioida nyt tämä 1
arvioida sana tuntumaa 1
ei vaikuttaa kuu 1
erilainen tieto kielioppimalli 1
estimaatti ei vaikuttaa 1
estimaatti kielioppiaineisto laskea 1
estimaatti kumpi antaa 1
helmikuu tuntumaa jo 1
hyvä kumisaapas kevät 1
hyvä todennäköisyys oikea 1
ihminen suorituskyky kohta 1
ilma päihtyä turha 1
ja hyvä kumisaapas 1
ja soidinmeno aloittaa 1
jatkosana olla ja 1
jo seuraava sana 1
jo x arvioida 1
joka olla leuto 1
jolloin estimaatti ei 1
jotta se pystyä 1
järjestys kurkkia seuraava 1
kannattaa tehdä järjestys 1
kertyä tieto tehtävä 1
kevät ilma päihtyä 1
kielioppiaineisto laskea tasoittamaton 1
kielioppimalli tarvita jotta 1
kohta alkuperäinen lause 1
kohta jolloin estimaatti 1
koira öljyinen turku 1
koko lause alun, 1
konteksti peruste uudestaan 1
kumisaapas kevät ilma 1
kumpi antaa hyvä 1
kurkkia seuraava kohta 1
kuu se mennä 1
laskea tasoittamaton estimaatti 1
lause alun, joka 1
lause olla sana 1
leuto sää ja 1
löytyä paperi kääntöpuoli 1
mahdollinen jatkosana olla 1
mennä kertyä tieto 1
mikä erilainen tieto 1
nyt tämä konteksti 1
oikea sana tietää 1
olla arvioida sana 1
olla ja hyvä 1
olla leuto sää 1
olla saada helmikuu 1
olla sana löytyä 1
peruste uudestaan antaa 1
pystyä vastata ihminen 1
päihtyä turha koira 1
saada helmikuu tuntumaa 1
sana löytyä paperi 1
sana tietää koko 1
sana todennäköisyys mahdollinen 1
sana todennäköisyys mikä 1
sana tuntumaa jo 1
se mennä kertyä 1
se pystyä vastata 1
seuraava kohta jolloin 1
seuraava sana todennäköisyys 1
soidinmeno aloittaa tiainen 1
suorituskyky kohta alkuperäinen 1
sää ja soidinmeno 1
tarvita jotta se 1
tasoittamaton estimaatti kumpi 1
tehdä järjestys kurkkia 1
tehtävä kannattaa tehdä 1
tehtävä olla arvioida 1
tiainen olla saada 1
tieto kielioppimalli tarvita 1
tieto tehtävä olla 1
tietää koko lause 1
todennäköisyys mahdollinen jatkosana 1
todennäköisyys mikä erilainen 1
todennäköisyys oikea sana 1
tuntumaa jo seuraava 1
tuntumaa jo x 1
turha koira öljyinen 1
turku verrata antaa 1
tämä konteksti peruste 1
tämä tehtävä kannattaa 1
uudestaan antaa sana 1
vaikuttaa kuu se 1
vastata ihminen suorituskyky 1
verrata antaa estimaatti 1
x arvioida nyt 1
öljyinen turku verrata 1

Tasoittamattomat estimaatit saadaan suoraan laskemalla kunkin n-grammin osuus kaikista havaituista n-grammeista:

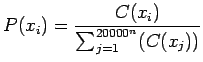
$\displaystyle P(x_i)=\frac{C(x_i)}{\sum_{j=1}^{20000^n} ( C(x_j))}$ (1)

Tämä estimaatti asettaa nollatodennäköisyyden kaikille havaitsemattomille n-grammeille. Mallin antamat estimaatit on annettu taulukossa 2.

Taulukko: Todennäköisyysestimaatit, suurin uskottavuus
esiintyi opetuksessa unigrammit bigrammit trigrammit
0      
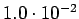
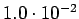
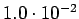
1 $ 1.0\cdot 10^{-2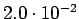}$ $ 1.0\cdot 10^{-2}$ $ 1.0\cdot 10^{-2}$
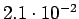
2 $ 2.0\cdot 10^{-2}$ $ 2.1\cdot 10^{-2}$  
3 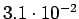$ 3.1\cdot 10^{-2}$    
4      
5 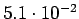$ 5.1\cdot 10^{-2}$    


b)
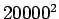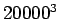Tehtävässä annettiin, että käytettävä sanaston koko olisi 20000. Tämä tarkoitta esim. unigrammejen kohdalla sitä, että kaikkia sanoja käsitellään niinkuin ne olisi nähty kerran useammin kuin ne oikeasti nähtiin. Bigrammien ja trigrammien kohdalla tehdään samalla tavalla, mutta niitä on tietysti paljon enemmän, bigrammeja $ 20000^2$ ja trigrammeja $ 20000^3$. Kunkin n-grammin todennäköisyys saadaan siis kaavasta

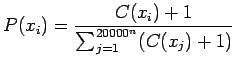
$\displaystyle P(x_i)=\frac{C(x_i)+1}{\sum_{j=1}^{20000^n} ( C(x_j)+1)}$ (2)

Taulukossa 3 on esitetty tulokset niin, että vasempaan sarakkeen on merkattu kuinka monta kertaa n-grammi esiintyi tekstissä ja seuraaviin sarakkeisiin vastaavat todennäköisyysestimaatit.

Taulukko: Todennäköisyysestimaatit, Laplace
esiintyi opetuksessa unigrammit bigrammit trigrammit
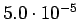
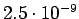
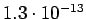
0 $ 5.0\cdot 1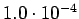0^{-5}$ $ 2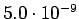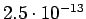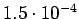.5\cdot 10^{-9}$ $ 1.3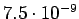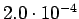\cdot 10^{-13}$
1 $ 1.0\cdot 10^{-4}$ $ 5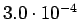.0\cdot 10^{-9}$ $ 2.5\cdot 10^{-13}$
2 $ 1.5\cdot 10^{-4}$ $ 7.5\cdot 10^{-9}$  
3 $ 2.0\cdot 10^{-4}$    
4      
5 $ 3.0\cdot 10^{-4}$    


c)
Lidstonen tasoitus on kuin Laplacen tasoitus, paitsi yhden sijasta lisätään 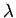$ \lambda$ jo nähtyä näytettä. Lambda pitäisi valita niin, että estimaatit pysyvät järkevinä, mutta että liikaa todennäköisyyttä ei sijoiteta havaitsemattomille tapauksille. Tässä tehtävässä 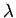$ \lambda$ on valittu pahasti alakanttiin.

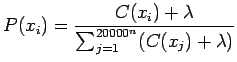
$\displaystyle P(x_i)=\frac{C(x_i)+\lambda}{\sum_{j=1}^{20000^n} ( C(x_j)+\lambda)}$ (3)


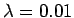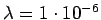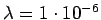
Taulukko: Todennäköisyysestimaatit, Lidstone, unigrammejen $ \lambda = 0.01$, bigrammejen $ \lambda =1\cdot 10^{-6}$, trigrammejen $ \lambda =1\cdot 10^{-6}$
esiintyi opetuksessa unigrammit bigrammit trigrammit
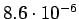
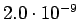
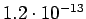
0 $ 8.6\cdot 1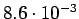0^{-6}$ $ 2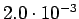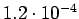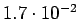.0\cdot 10^{-9}$ $ 1.2\cdot 10^{-13}$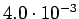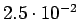
1 $ 8.6\cdot 10^{-3}$ $ 2.0\cdot 10^{-3}$ $ 1.2\cdot 10^{-4 }$
2 $ 1.7\cdot 10^{-2}$ $ 4.0\cdot 10^{-3}$  
3 $ 2.5\cdot 10^{-2}$    
4      
5 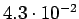$ 4.3\cdot 10^{-2}$    


Katsotaanpa vielä, kuinka paljon kukin malli sijoitti todennäköisyysmassa havaitsemattomille näytteille (taulukko 5). Huomataan, että näin pienellä opetusjoukolla Laplace sijoittaa lähes kaiken todennäköisyysmassan tuntemattomille näytteille. Lidstonen painokertoimella $ \lambda$ saadaan säädettyä, kuinka paljon se laittaa todennäköisyyttä tuntemattomille, mutta jos $ \lambda$ pistetään kovin pieneksi (kuten tässä tehtiin), malli tuskin toimii kovin hyvin testiaineistolla.

Taulukko: Havaitsemattomien näytteiden todennäköisyysmassa
menetelmä havaitsemattomien osuus %
unigram, Laplace 91.6
unigram, Lidstone 17.2
bigram, Laplace 100.0
bigram, Lidstone 80.6
trigram, Laplace 100.0
trigram, Lidstone 98.8


3.
Tarkoituksenamme siis on laskea todennäköisyyksiä nähdyille trigrammeille. Tavallinen suuriman uskottavuuden estimaattihan olisi

$\displaystyle p(x)=\frac{r}N$ (4)

missä $ r$ kertoo, kuinka monta kertaa sana esiintyi ja N on kaikkien sanojen lukumäärä. Good-Turing estimaatissa käytetään korjattua estimaattia $ r^*$:

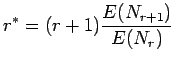$\displaystyle r^*=(r+1)\frac{E(N_{r+1})}{E(N_r)}$ (5)

Good-Turing -tasoitusta voi intuitiivisesti ajatella vaikka niin, että kuvitellaan kaikkia yksiköitä nähdyksi hieman vähemmän kertoja kuin ne oikeasti nähtiin. Eli jos trigrammi nähtiin 10 kertaa, leikitään että se nähtiinkin vain 9.1 kerran. Jos trigrammi nähtiin kerran, leikitään että se nähtiin 0.5 kertaa. Oletetaan että on olemassa $ N_1$ trigrammia, joita ei nähty ja leikitään, että ne nähtiin 0.3 kertaa. Tämä ei tietysti ole matemaattisiseti aivan eksakti määritelmä, mutta helpottaa ehkä tehtävän seuraamista.

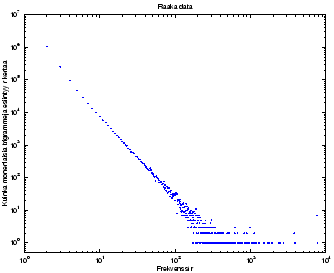
Good-Turing -tasoituksen laskeminen aloitetaan taulukoimalla, kuinka monta kertaa eri trigrammia on nähty $ r$ kertaa (esim. aineistossa oli 7462 trigrammia, jotka kaikki esiintyivät 10 kertaa). Tästä taulukosta on piiretty kuvaaja 1.

Kuva: X-akseli: esiintymisfrekvenssi. Y-akseli: Kuinka monta trigrammia on esiintynyt $ r$ kertaa.
\begin{figure}\centering\epsfig{file=GTraaka.eps,width=0.6\linewidth}\end{figure}

Huomataan, että tähän käyrään olisi helppo sijoittaa suora viiva, paitsi että suuremmilla frekvensseillä tapahtuu jotain kummaa: trigrammeja, joita on esiintynyt vaikkapa 500 kertaa on joko 0 tai 1 kappale. Eli lopussa ei ole enää tasaista käyrää, vaan vain diskreettejä arvoja 0 ja 1. Kokeillaan tasoitella käyrän loppupäätä levittämällä todennäköisyysmassaa tasaisesti koko ympäristöön. Esim. jos trigrammi on esiintynyt 510 kertaa, mutta seuraavaksi yleisin trigrammi on esiintynyt 514 kertaa, jaetaan tuo 1 koko välille, eli kaikille frekvensseille 510-514 tulee arvoksi $ \frac1{514-510}$. 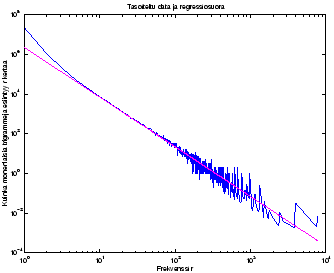Katsotaan, miltä kuvaaja näyttää tämän jälkeen. Kuvassa 2 nähdään tasoitettu data ja siihen sovitettu suora. Suora sovitettiin kummankin muuttujan logaritmeihin, jolloin se saatiin kauniisti myötäilemään datan muotoa.

Kuva: Tasoitettu kuva ja logaritmisella asteikolla sovitettu suora.
\begin{figure}\centering\epsfig{file=GTsmooth.eps,width=0.6\linewidth}\end{figure}

Matalat $ r$:n arvot ovat paremmin arvioidut koska niihin meillä on ollu paljon dataa. Käytetään siis niiden arvioina suoraan taulukossa olleita arvoja ja katsotaan korkeat $ r$:n arvot suoraan käyrältä. Tässä tehtävässä päätin käyttää suoralta luettuja arvoja, kun $ r>15$.

Vielä pitäisi antaa jonkinverran todennäköisyysmassa trigrammeille, joita ei ole vielä nähty. Good-Turing estimaatissa näille annetaan yhteensä $ \frac{N_1}{N}$ todennäköisyyttä. Tämä todennäköisyys voitaisiin jakaa vaikkapa aineistosta opetetulle bigrammimallille. Nyt, jos trigrammimalli ei osaa antaa sanalle todennäköisyyttä, voidaan tätä todennäköisyyttä kysyä bigrammimallilta. Tuntemattomille bigrammeille jäävä todennäköisyysmassa voitaisiin taas puolestaan jakaa unigrammimallille. Tuntemattomille unigrammeille jäävästä todennäköisyydestä voidaan vain todeta, että tässä on todennäköisyys, että tulee vastaan sana, jota malli ei tunne. Tällainen perääntyvä (back-off) kielimalli on käytössä esim. lähes kaikissa suuren sanaston puheentunnistimissa. Tässä esitettiin vain perusidea perääntyvien kielimallejen estimoinnille. Käytännössä se ei ole aivan näin suoraviivaista.

Kun nyt laskemme korjatulla $ r^*$:llä kaavan 4 mukaan todennäköisyydet saamme melko estimaatit eri sanojen todennäköisyyksille. Taulukkoon 6 on merkitty muutamalle eri r:lle todennäköisyydet. Opetetun mallin mielestä 81% todennäköisyydestä on tuntemattomilla trigrammeilla. Tämä on suomen kielelle melko uskottavan kuuloinen tulos, sillä suomen kielen sanamäärä on niin suuri, että kielelle on käytännössä mahdotonta tehdä kattavaa trigrammimallia. Sivuhuomatuksena mainittakoon, että trigrammimallinnus voi soveltaa suomen kieleen myös hajoittamalla sanat vaikkapa morfeemeiksi ja opettamalla trigrammimalli näiden pienempien palojen yli.


Taulukko: Good-Turing todennäköisyysestimaatit
$ r$ todennäköisyys
1 $ 1.9\cdot 10^{-10}$
2 $ 3.3\cdot 10^{-9 }$
3 $ 2.5\cdot 10^{-8 }$
10 $ 2.7\cdot 10^{-7 }$
50 $ 1.7\cdot 10^{-6 }$
100 $ 3.5\cdot 10^{-6 }$
573 $ 2.0\cdot 10^{-5 }$
1327 $ 4.7\cdot 10^{-5 }$


4.
Muutetaan hämmentyneisyyden (perplexity) kaavaa niin, että voidaan suoraan käyttää log-todennäköisyyksiä:

$\displaystyle perp(w_1,w_2,\dots,w_N)$ $\displaystyle =$ $\displaystyle \prod_{i=0}^NP(w_i\vert w_{i-1},\dots,w_1)^{-\frac1N}$  
  $\displaystyle =$ $\displaystyle \prod_{i=0}^N 10^{-\frac1N \log(P(w_i\vert w_{i-1},\dots,w_1))}$  
  $\displaystyle =$ $\displaystyle 10^{-\frac1N \sum_{i=0}^N \log(P(w_i\vert w_{i-1},\dots,w_1))}$  


Lasketaan summa erikseen:

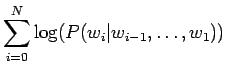    $\displaystyle \sum_{i=0}^N \log(P(w_i\vert w_{i-1},\dots,w_1))$  
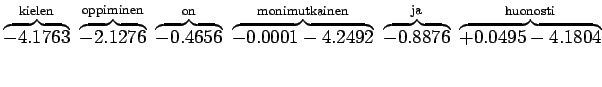  $\displaystyle =$ $\displaystyle \overbrace{-4.1763}^{\textrm{kielen}} ~\overbrace{-2.1276}^{\text... ...verbrace{-0.8876}^{\textrm{ja}} ~\overbrace{+0.0495-4.1804}^{\textrm{huonosti}}$  
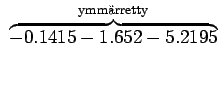    $\displaystyle ~\overbrace{-0.1415-1.652-5.2195}^{\textrm{ymmärretty}}$  
  $\displaystyle =$ $\displaystyle -21.5734$  

Niille sanoille, joille ei löytynyt trigrammimallia, jouduttiin käyttämään sekä perääntymiskerrointa että todennäköisyyttä. Jos myöskään bigrammimallia ei löytynyt, jouduttiin vielä kerran perääntymään.

Sijoitetaan vielä luvut hämmentyneisyyden lausekkeeseen

$\displaystyle perp(w_1,w_2,\dots,w_N)=10^{-\frac1N \frac{-21.5734}{-7}}\approx 1200$      

Tulosta voi ajatella vaikka niin, että kielimalli vastaa sellaista kielimallia, joka joutuu valitsemaan 1200 yhtä todennäköisen sanan väliltä (ei ihan eksaktisti paikkansapitävä väite).

Sana 'tapahtumaketju' ei ollut 64000 yleisimmän sanan joukossa ja ei sisältynyt siis kielimalliin. Kielimallin ohi meni siis $ \frac18\approx13\%$ sanoista.


vsiivola@cis.hut.fi