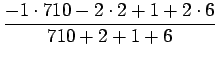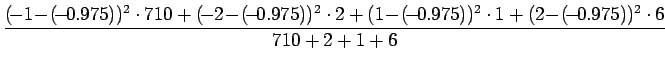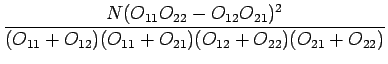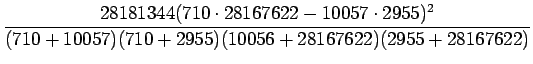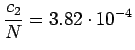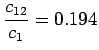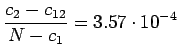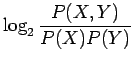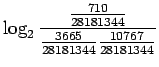T-61.281 Luonnollisten kielten tilastollinen käsittely

Vastaukset 3, ti 11.2.2003, 16:15-18:00 - Kollokaatiot, Versio 1.1

1.

Lasketaan ensin tulokset sanaparille ``valkoinen'',''talo'' käsin:

• Frekvenssimenetelmä: Bigrammeja ``valkoinen'',''talo'' oli 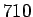$710$ kappaletta.
• Normalisoitu frekvenssimenetelmä: Sana ``valkoinen'' esiintyi 3665 kertaa ja sana ``talo'' 10767 kertaa. Vertailuluvuksi saadaan $\frac{710}{3665\cdot 10767} \approx 1.8\cdot 10^{-5}$.

Kaikkien sanojen tulokset frekvenssimenetelmälle on esitetty taulukossa 1.

Taulukko: Frekvenssimenetelmän tulokset

$s_1$	$s_2$	$C(s_1,s_2)$
ja	olla	7329
venäjä	presidentti	717
valkoinen	talo	710
kova	tuuli	279
aste	pakkanen	160
tuntematon	sotilas	154
sekä	myös	138
liukas	keli	106
hakea	työ	31
oppia	lukea	21
ottaa	onki	9
vihainen	mielenosoittaja	7
olla	ula	5
heittää	veivi	3
herne	nenä	3

Taulukko: Normalisoidun frekvenssimenetelmän tulokset

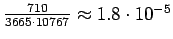$s_1$	$s_2$	Normalisoitu frekvenssi $\cdot10^{-8}$
liukas	keli	1981
aste	pakkanen	386
heittää	veivi	293
herne	nenä	268
valkoinen	talo	180
tuntematon	sotilas	163
vihainen	mielenosoittaja	68
kova	tuuli	35
ottaa	onki	21
venäjä	presidentti	10
oppia	lukea	8
hakea	työ	1
olla	ula	0
sekä	myös	0
ja	olla	0

Huomataan, että jo ``hihasta ravistetuilla'' menetelmillä päästään kohtalaisiin tuloksiin.

2.

Lasketaan käsin malliksi tulos jo tutulle kollokaatiolla ``valkoinen'', ``talo''. Keskiarvo:

$$Mean(\textrm{\lq\lq valkoinen''},\textrm{''talo''}) = \frac{-1\cdot 710 -2 \cdot 2 + 1 + 2 \cdot 6 } {710 +2+1 + 6 }$$

$$\approx -0.975$$

Varianssi

$$Var(\textrm{\lq\lq valkoinen''},\textrm{''talo''})$$

$$= \frac{(\!-1\! - \!(\!-\!0.975))^2\cdot710 +(\!-2\!-\!(\!-\!0.975)... ...+ (1\!-\!(\!-\!0.975))^2\cdot1 + (2\!-\!(\!-\!0.975))^2\cdot6 } {710 +2+1 + 6 }$$

$$\approx 0.083$$

Lopuille sanoille tulokset on annettu varianssin mukaan järjestettynä taulukossa 3.

Taulukko: Pienimmän varianssin mukaan järjestetyt tulokset

$s_1$	$s_2$	Keskiarvo	Varianssi
herne	nenä	-1.000	0.000
vihainen	mielenosoittaja	-1.000	0.000
tuntematon	sotilas	-1.025	0.025
valkoinen	talo	-0.975	0.083
ottaa	onki	-1.250	0.188
venäjä	presidentti	-1.128	0.472
kova	tuuli	-0.880	0.492
liukas	keli	-0.788	0.608
oppia	lukea	-0.606	1.087
heittää	veivi	-0.500	1.250
aste	pakkanen	-0.465	1.347
hakea	työ	-0.433	2.046
olla	ula	-0.250	2.438
sekä	myös	0.252	2.981
ja	olla	-0.083	3.635

Taulukkoa tarkastellessamme huomaamme, että menetelmä on löytänyt käytännössä kaikki kiinteät kollokaatiot, kuten valkoinen talo. Menetelmä ei pärjää hyvin harvalla aineistolla, esin. vihainen mielenosoittaja ei selvästikään ole kollokaatio, vaikka menetelmä ensimmäiseksi sijoittaakin.

Tarkasteluikkunan leveys vaikuttaa tietysti alueeseen, josta kollokaatioita etsitään. Jos aluetta kasvatetaan liian suureksi, rupeavat sanat esiintymään yhä useammin myös satunnaisesti yhdessä ja varianssi kasvaa suureksi. Liian pienellä ikkunalla ei pitempivaikutteisia kollokaatioita löydetä. Jos kollokaation toinen sana voi olla sekä referenssisanan edessä että takana, menetelmä tietysti hämääntyy täydellisesti.

3.

$\chi ^2$-testi perustuu yksinkertaiselle perusoletukselle. Katsotaan annettujen sanojen esiintymistodennäköisyydet ja lasketaan niiden perusteella, kuinka monta kertaa sanojen pitäisi esiintyä yhdessä. Tätä lukua verrataan havaittuun lukuun ja jos nämä pikkeavat suuresti toisistaan, todetaan että sanojen pitää olla kollokaatioita.

Aloitetaan kasaamalla seuraavanlainen taulukon (taulukko 4):

Taulukko: $\chi ^2$-testissä tarvittavia suureita.

	$w_1$=valkoinen	$w_1 \ne$ valkoinen
$w_2=$talo	710 (valkoinen talo)	$10767-710=10057$ (punainen talo)
$w_2\ne$talo	$3665-710=2955$ (valkoinen mopo)	$28181344-710-10057-2955=28167622$ (punainen pappi)

Nämä arvot voidaan sijoittaa sitten kahden muuttujan $\chi ^2$-testin kaavaan:

$$\chi^2 = \frac{N(O_{11}O_{22}-O_{12}O_{21})^2} {(O_{11}+O_{12})(O_{11}+O_{21})(O_{12}+O_{22})(O_{21}+O_{22})}$$

Luvut sijoittamalla saadaan siis:

$$\chi^2 = \frac{28181344(710\cdot28167622 -10057\cdot 2955)^2} {(710+10057)(710+2955)(10056+28167622)(2955+28167622)}$$

$$\approx 358771$$

Jos $\chi ^2$-testin tulos on yli 3.843, näyte on vedetty alle 5% todennäköisyydellä riippumattomasta jakaumasta. Tässä siis valkoinen talo vaikuttaa kollokaatiolta. Kuitenkin kun katsomme taulukkoa 5, huomaamme että melkein kaikki sanat olisivat sen mukaan kollokaatioita. $\chi ^2$-testihän ei testaa sitä, ovatko sanat kollokaatioita, vaan sitä että ovatko sanat riippumattomia. Esimerkiksi sanapari ``ja'', ``olla'' on melko korkealla tuloksissa, sillä näiden kahden sanan välillä esiintyy negatiivinen korrelaatio: sanat esiintyvät harvemmin peräkkäin kuin niiden satunnaisuuden mukaan pitäisi. Tätä riippuvuutta ei voida tietysti pitää merkkinä siitä, että sanat olisivat kollokaatioita.

Taulukko: $\chi ^2$-testin tulokset

$s_1$	$s_2$	$\chi ^2$
liukas	keli	591591
valkoinen	talo	358771
aste	pakkanen	173726
tuntematon	sotilas	70409
ja	olla	29194
kova	tuuli	26644
venäjä	presidentti	18147
heittää	veivi	4120
herne	nenä	2258
vihainen	mielenosoittaja	1321
ottaa	onki	525
oppia	lukea	449
hakea	työ	47
sekä	myös	45
olla	ula	0

Viimeksi pyydettiin vielä laskemaan uskottavuussuhdetestillä järjestys sanoille. Uskottavuussuhdetestissä tarkastellaan kahden eri hypoteesin uskottavuuden suhdetta:

$H_1$:

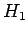sanat esiintyvät satunnaisesti toisistaan riippumatta

$H_2$:

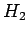sanojen esiintyminen riippuu toisistaan

Uskottavuussuhdetestin laskemiseen tarvitaan seuraavia suureita (luvut ovat tehtävän sanoille ``valkoinen'' ja ``talo''):

$$c_1 = C(s_1) =3665$$

$$c_2 = C(s_2) =10767$$

$$c_{12} = C(s_1,s_2) =710$$

$$p = \frac{c_2}{N} = 3.82\cdot 10^{-4}$$

$$p_1 = \frac{c_{12}}{c_1} =0.194$$

$$p_2 = \frac{c_2-c_{12}}{N-c_1} = 3.57\cdot 10^{-4}$$

Jos oletetaan sanoille binomijakauma

$$b(k,n,x)={n \choose k}x^k(1-x)^{n-k},$$

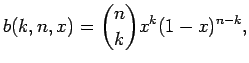voidaan uskottavuuksien suhde kirjoittaa (tarkempi johto kirjassa, katso myös sieltä lainattu taulukko 6)

Taulukko: Uskottavuustestin laskennassa käytettäviä suureita.

$$	$H_1$	$H_2$
$P(w_2\vert w_1)$	$p=\frac {c_2}N$	$p_1 = \frac {c_{12}}{c_1}$
$P(w_2\vert\textrm{ ei } w_1)$	$p=\frac {c_2}N$	$p_2=\frac{c_2-c_{12}}{N-c_1}$
$P(c_{12} \vert c_1)$	$b(c_{12},c_1,p)$	$b(c_{12},c_1,p_1)$
$P(c_2- c_{12} ~ \vert N-c_1 )$	$b(c_2-c_{12},N-c_1,p)$	$b(c_2-c_{12},N-c_1,p_2)$

$$\log \lambda = \log \frac{L(H_1)}{L(H_2)}$$

$$= \log \frac{b(c_{12},c_1,p)b(c_2-c_{12},N-c_1,p)} {b(c_{12},c_1,p_1)b(c_2-c_{12},N-c_1,p_2)}$$

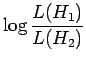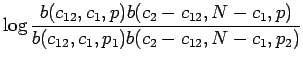Tässähän lasketaan kullekin hypoteesille datan uskottavuus kahdessa osassa. Ensin lasketaan todennäköisyys niille bigrammeille, joissa ensimmäinen sana on ``valkoinen'' (näistä $c_{12}$ tapauksessa seuraa sana ``talo'') ja sitten todennäköisyys datan bigrammeille, joissa ensimmäinen sana ei ollut ``valkoinen'' (näistä $c_2-c_{12}$ tapauksessa seuraava sana on ``talo''). Ensimmäisen hypoteesin mukaan kummassakin tapauksessa todennäköisyys $p$ on sama, sillä sanat ovat riippumattomia. Toisen hypoteesin mukaan todennäkösyydet ovat erilaiset ($p_1$, $p_2$). Testissä lasketaan näiden datan todennäköisyyksien suhde.

Määritellään vielä funktio $F$:

$$F(k,n,x) = x^k(1-x)^{n-k}$$

$$\log F(k,n,x) = k\log(x)+(n-k)\log(1-x)$$

Nyt voidaan uskottavuuksien suhde laskea kaavasta

$$\log \lambda = \log F(c_{12},c_1,p)+\log F(c_{2}-c_{12},N-c_1,p)$$

$$-\log F(c_{12},c_1,p_1) -\log F(c_{2}-c_{12},N-c_{1},p_2)$$

Sijoitellaan lukuja

$$\log \lambda = \log L(710,3665,3.82\cdot10^{-4})$$

$$+ \log L(10767-710,28181344-3655,3.82\cdot10^{-4})$$

$$-\log L(710,3665,0.194 )$$

$$-\log L(3665-710,28181344-2665,3.57\cdot 10^{-4})$$

$$\approx -3811$$

Kun katsomme uskottavuussuhdetestin tuloksia (taulukko 7), huomaamme että myös tässä testi ei testaa sitä, ovatko sanat kollokaatioita, vaan sitä ovatko ne riippumattomia. Tuloksia voidaan perustella samoin argumentein kuin $\chi ^2$ testin kohdalla.

Taulukko: Uskottavuussuhdetestin tulokset

$s_1$	$s_2$	$L$
ja	olla	-21567
valkoinen	talo	-3811
venäjä	presidentti	-1696
kova	tuuli	-1013
aste	pakkanen	-972
liukas	keli	-824
tuntematon	sotilas	-799
oppia	lukea	-46
vihainen	mielenosoittaja	-30
heittää	veivi	-29
ottaa	onki	-28
sekä	myös	-26
herne	nenä	-17
hakea	työ	-15
olla	ula	0

4.

Yhteisinformaatio kertoo, kuinka paljon lisätietoa $X$:n haivaitseminen antaa $Y$:stä. Jos $X$ ja $Y$ ovar riippumattomia, yhteisinformaatio on nolla. Lasketaan käsin malliksi tulos sanaparille ``valkoinen'',''talo''.

$$I(x,y) = \log_2\frac{P(X,Y)}{P(X)P(Y)}$$

$$= \log_2\frac{\frac{710}{28181344}}{\frac{3665}{28181344}\frac{10767}{28181344}}$$

$$\approx 9.0$$

Tulokset koko sanajoukolle on esitetty taulukossa 8.

Taulukko: Yhteisinformaation mukaan järjestetyt tulokset

$s_1$	$s_2$	MI
liukas	keli	12.4
aste	pakkanen	10.1
heittää	veivi	9.7
herne	nenä	9.6
valkoinen	talo	9.0
tuntematon	sotilas	8.8
vihainen	mielenosoittaja	7.6
kova	tuuli	6.6
ottaa	onki	5.9
venäjä	presidentti	4.8
oppia	lukea	4.5
hakea	työ	1.7
olla	ula	0.5
sekä	myös	-0.8
ja	olla	-2.5

Tulokset vaikuttavat hyviltä. Hieman kommenttia kirjan kritikkiin, että menetelmä erityisesti suosisi harvinaisia sanoja: Yksi tekijä joka tähän johtaa, on laskussa käytettyjen todennäköisyyksien estimointi - tässä käytetään maksimiuskottavuusestimaattoreita. Paremman tuloksen saa varmasti, jos asettaa sanapareille priorin, että en ovat riippumattomia ja antaa datan sitten muokata tätä oletusta.

Yhteenvetona koko laskarista voisi sanoa vaikka seuraavaa: Heuristisilla menetelmillä (1. ja 2. tehtävä) voidaan päästä yksinkertaisissa tapauksissa kohtalaisiin tuloksiin. Perinteinen tilastomatematiikka (tehtävä 3) voi olla hieman epäintuitiivista, jos sitä ei ole tottunut käyttämään. Suoraan todennäköisyyteen perustuvat menetelmät (tehtävät 4 ja 5) ovat ehkä intuitiivisesti selkeämpiä ja koska ne perustuvat todennäköisyyslaskuun, niissä on helppo ottaa huomioon monia tekijöitä. Esitettyjen todennäköisyyteen perustuvien menetelmien tulokset olisivat varmastikin luotettavimpia etenkin pienemmillä datamäärillä, jos suurimman uskottavuuden (ML) estimaattien sijaan käytettäisiin vaikkapa maksimi a posteriori (MAP) estimaatteja.