T-61.281 Luonnollisten kielten tilastollinen käsittely
Vastaukset 11, ti 8.4.2003, 16:15-18:00 Klusterointi, Konekääntäminen. Versio 1.0

1.
Kuvaan 1 on piirretty klusteroinnit käyttäen annettuja algoritmeja. Sanojen yhdistämisjärjestys on merkitty numeroilla vastaavien viivojen viereen ja kutakin yhdistämistä vastaava etäisyys on merkitty kuvassa olevaan taulukkoon. Single link-klusteroinnissa etäisyydet lasketaan yhdistettävien ryhmien lähimpien alkioiden välillä. Complete link-klusteroinnissa taas etäisyys lasketaan kaukaisimpien alkioiden välillä.

Kuva: Vasemmalla Single link, oikealla Complete link. Lasketaessa complete link-klusterointia, olisi viidentenä yhdistämisenä voitu yhdistää ryhmään (kaivuri,zetor) joko ryhmä (puukko, tuppi) tai ryhmä (kenraali), sillä molemmat ovat yhtä kaukana. Tässä tapauksessa siihen yhdistettiin ryhmä (kenraali).
\begin{figure}\epsfig{file=single_link.eps,width=0.49\textwidth}\hfill \epsfig{file=complete_link.eps,width=0.49\textwidth} \end{figure}

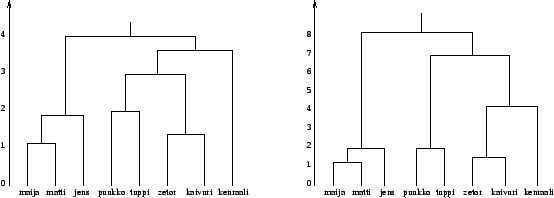
Piirretään vielä klusterointeja vastaavat dendrogammit. Dendrogrammissa on pystysuunnassa etäisyysasteikko, ja aina kun kaksi ryhmää yhdistetään, se merkitään tälle etäisyydelle (Kuva 2).

Kuva: Vasemmalla Single link, oikealla Complete link.
\begin{figure}\epsfig{file=single_dendro.eps,width=0.45\textwidth}\hfill \epsfig{file=complete_dendro.eps,width=0.45\textwidth} \end{figure}

Nyt kun haluamme muodostaa klusterit, meidän pitäisi vielä dendrogrammista osata päätellä, mikä etäisyys laitetaan raja-arvoksi klustereiden muodostumiselle. Nyt vaikuttaisi siltä, että sekä single link, että complete link -klusteroinnille sopiva raja-arvo olisi noin 2.9. Tämän rajan alapuolella molemmat menetelmät antavat saman klusteroinnin (Taulukko 1).

Taulukko 1: Ryhmittely
ryhmä sanat
1 matti, maija, jens
2 puukko, tuppi
3 kaivuri, zetor
4 kenraali


2.
K-means algoritmi toimii jotakuinkin seuraavalla tavalla:
1)
Päätetään kuinka monta klusteria halutaan löytää
2)
Sijoitetaan alkuperäiset klusterikeskukset jollain tavalla avaruuteen (esim. arpomalla järkevälle alueelle datapilven sisään)
3)
Merkitään kaikille datapisteille, mikä klusterikeskus on sitä lähinnä
4)
Siirretään klusterikeskusta: lasketaan niiden näytteiden paikan keskiarvo, joille klusterikeskus on lähin ja siirretään klusterikeskus sinne
5)
Tarkistetaan, täyttyikö lopetusehto (esim. klusterointi ei muuttunut). Jos ei, palataan askeleeseen 3.

Tässä tehtävässä siis etsitään kolmea klusteria, klustereiden alustava sijainti on annettu. Kuvassa 3 esitetään algoritmin kulku.

Kuva: Vasemmalla on on lähtötilanne. Datapisteet on merkitty palloilla ja klusterikeskukset tähdillä. Datapiste on yhdistetty lähimpään klusterikeskukseen viivalla. Toisessa kuvassa klusterit on siirretty ja näille siirretyille keskuksille on etsitty lähimmät naapurit. Kolmannessa kuvassa iterointi jatkuu ja neljänteen kuvaan saavuttaessa ei muutoksia enää tapahdu.
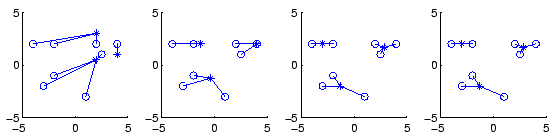\begin{figure}\epsfig{file=kmeans.ps,width=\textwidth}\end{figure}

Tässä saatiin siis taulukossa 2 nähtävät klusterit.

Taulukko: k-means -ryhmittely
ryhmä sanat
1 matti, maija, jens
2 puukko, tuppi
3 kaivuri, zetor, kenraali


3.
a)
Kuvaan 4 on piirretty annettu data. Knn-tunnistimen naapureiden määräksi valittiin 3. Tämä tarkoittaa sitä, että etsitään kunkin luokiteltavan sanan kolme lähintä naapuria ja nämä äänestävät siitä, mihin luokkaan sana laitetaan.

Kuva: Data. Verbit on merkitty laatikoilla, substantiivit ympyröillä ja luokiteltavat sanat tähdellä.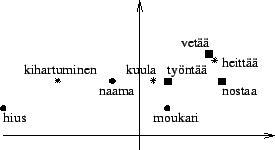
\begin{figure}\begin{center} \leavevmode \epsfig{file=knn.eps,width=0.5\textwidth} \end{center} \end{figure}

Katsotaanpa ensinnä sanaa kihartuminen. Sen kolme lähintä tunnettu naapuria ovat hius, naama ja työntää. Vastaavat äänet ovat S,S ja V eli sana luokitellaan substantiiviksi.

Sanalle kuula lähimmät naapurit ovat työntää, moukari ja naama. Näin ollen se luokitellaan substantiiviksi.

Sana heittää naapurit vetää, nostaa ja työntää ovat yksimielisiä siitä, että sana on verbi.

b)
Korvataan kukin luokka sen keskipisteellä. Verbien keskipiste on 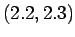$ (2.2, 2.3)$ ja substantiiveille se on 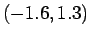$ (-1.6, 1.3)$. Nyt sanaa heittää lähinnä on verbien keskipiste, sanaa kihartuminen substantiivejen ja sanaa kuula lähinnä verbien keskipiste.

c)
b-kohdan menetelmässä korvataan yksittäiset datapisteet niitä kaikkia yhteiseti edustavalla prototyypillä. Tämä vähentää tuntuvasti luokittelussa tarvittavien laskutoimitusten määrää (sen sijaan että luokiteltavan sana etäisyys pitää laskee kaikille sanoille, riittää että se lasketaan keskiarvoille). Joissain tapauksissa tällainen prototyyppimalli myös yleistää paremmin.

Tässä tapauksessa nähdään menetelmän huono puoli: Se ei pysty esittämään monimutkaisemman datapilven muotoa yhtä hyvin kuin siinä olevat datapisteen erikseen lueteltuna ja tässä luokittelee sanan kuula väärin.

4.
Lähdetään liikkeelle trigrammitodennäköisyydestä:
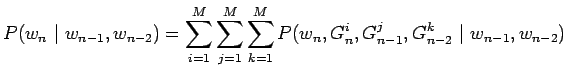$\displaystyle P(w_n~\vert~w_{n-1},w_{n-2}) = \sum_{i=1}^M \sum_{j=1}^M \sum_{k=1}^M P(w_n,G_n^i,G_{n-1}^j,G_{n-2}^k~\vert~ w_{n-1}, w_{n-2})$      

Tässä siis $ G_n$ kuvaa sanan $ w_n$ ryhmää. Mahdollisia ryhmiä on $ M$ kappaletta. Oletetaan, että sana voi kuulua vain yhteen ryhmään. Hajoitetaan summan sisällä oleva lauseke käyttäen todennäköisyyslaskun kaavaa $ P(A,B~\vert~C)=P(A~\vert~B,C)P(B~\vert~C)$.
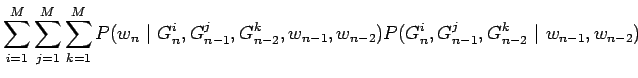$\displaystyle \sum_{i=1}^M \sum_{j=1}^M \sum_{k=1}^M P(w_n ~\vert~ G_n^i,G_{n-1... ...n-2}^k, w_{n-1}, w_{n-2}) P(G_n^i,G_{n-1}^j,G_{n-2}^k ~\vert~ w_{n-1}, w_{n-2})$      

Sievennetään ensimmäistä termiä olettamalla että sana $ w_n$ riippuu vain senhetkisestä ryhmästä $ G_n^i$. Jälkimmäinen termi voidaan jakaa samalla tavalla osiin kuin äskenkin tehtiin.
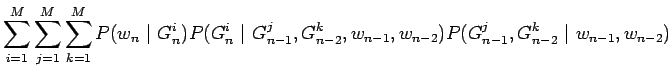$\displaystyle \sum_{i=1}^M \sum_{j=1}^M \sum_{k=1}^M P(w_n ~\vert~ G_n^i) P(G_n... ...^j,G_{n-2}^k, w_{n-1}, w_{n-2}) P(G_{n-1}^j,G_{n-2}^k ~\vert~ w_{n-1}, w_{n-2})$      

Nyt voimme sieventää toista termiä olettamalla, että nykyinen ryhmä $ G_n^i$ riippuu vain edeltävistä ryhmistä, mutta ei edeltävistä sanoista. Jaetaan viimeinen termi vielä tutulla tavalla osiin.

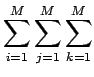$\displaystyle \sum_{i=1}^M \sum_{j=1}^M \sum_{k=1}^M$   $\displaystyle P(w_n ~\vert~ G_n^i) P(G_n^i ~\vert~ G_{n-1}^j,G_{n-2}^k) P(G_{n-1}^j ~\vert~ G_{n-2},w_{n-1},w_{n-2})$  
    $\displaystyle \cdot P(G_{n-2}^k ~\vert~ w_{n-1},w_{n-2})$  

Koska sana voi kuulua vain yhteen ryhmään, riippuu todennäköisyys
$ P(G_{x}^j ~\vert~ w_{x},\dots)$ vain sanasta $ w_{x}$ ja on yksi, kun on kyseessä ryhmä, johon sana kuuluu.

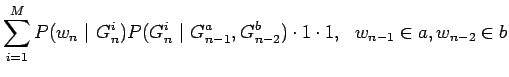$\displaystyle \sum_{i=1}^M P(w_n ~\vert~ G_n^i) P(G_n^i ~\vert~ G_{n-1}^a,G_{n-2}^b)\cdot1\cdot1, ~~ w_{n-1} \in a, w_{n-2} \in b$      

Koska $ w_n$ voi kuulua vain yhteen ryhmään $ G_n^c$, kaikki muut summan termi ovat nollia:
$\displaystyle P(w_n ~\vert~ G_n^c) P(G_n^c ~\vert~ G_{n-1}^a,G_{n-2}^b), ~~ w_n \in c, w_{n-1} \in a, w_{n-2} \in b$      

Tämä sievennetyn lausekkeen voisi ilmaista viellä hieman yksinkertaisemmin merkitsemällä $ G_x^{w_x}$:llä ryhmää, johon sana $ w_x$ kuuluu:

$\displaystyle P(w_n ~\vert~ G_n^{w_n}) P(G_n^{w_n} ~\vert~ G_{n-1}^{w_{n-1}},G_{n-2}^{w_{n-2}})$      

Mietitäänpä vielä lopuksi, mitä tällaisella approksimaatiolla saadaan aikaiseksi. Oletetaanpa vaikka, että meillä on 64000 sanasto, joista olemme muodostaneet 1000 klusteria. Nyt arvioitavien parametrien määrä on pudonnut $ 64000^3=2.6\cdot10^{14}$:sta $ 1000^3+64000=1\cdot10^9$:ään. Jos oletetaan, että sanat on hyvin klusteroitu ja klusterien väliset siirtymät kuvaavat lähes yhtä hyvin kuin sanojen väliset siirtymät, saadaan nämä parametrit myös arvioitua paljon paremmin kuin trigrammimallin parametrit (enemmän dataa per parametri). Jos klusterointi puolestaan on huono, eikä klusterista toiseen siirtyminen juurikaan vastaa sanoista toiseen siirtymistä, malli arvio vähäiset parametrinsa huonosti ja on todennäköisesti paljon heikompi malli kuin trigrammimalli. Edelleenkin tietysti parametrien määrä on paljon pienempi.

5.
Etsitään todennäköisin käännös $ \hat e$ ruotsinkieliselle lauseelle $ r$:

$\displaystyle \hat e = \qopname\relax m{argmax}_eP(e\vert r) = \qopname\relax m{argmax}_eP(e)P(r\vert e)$    

Käytetään kirjassa esitettyä mallia todennäköisyydelle $ P(r\vert e)$:

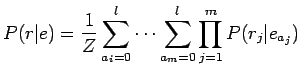$\displaystyle P(r\vert e)=\frac1Z \sum_{a_i=0}^l\cdots\sum_{a_m=0}^l \prod_{j=1}^m P(r_j\vert e_{a_j})$    

missä $ m$ on alkuperäisen ruotsinkielisen lauseen pituus ja $ l$ on käännetyn englanninkielisen lauseen pituus. Lasketaan kummallekin vaihtoehdolle:
$\displaystyle P(r\vert e_1)=1.0\cdot0.7\cdot0.9\cdot1.0\cdot1.0\cdot1.0\cdot0.1=0.063$      
$\displaystyle P(r\vert e_2)=1.0\cdot0.7\cdot1.0\cdot1.0\cdot1.0\cdot1.0\cdot1.0\cdot1.0=0.7$      

Tässä siis kokeillaan kaikkia käännössääntöjä jokaiselle ruotsinkielisen lauseen sanalle (huomioimatta sanajärjestystä). Koska säännöstö on hyvin harva, päästään näin yksinkertaiseen laskutoimitukseen.

Prioritodennäköisyys $ P(e)$ saadaan kielimallista. Lasketaan se kummallekin lauseelle:

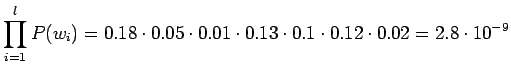$\displaystyle P(e_1)$ $\displaystyle =$ $\displaystyle \prod_{i=1}^l P(w_i) = 0.18\cdot0.05\cdot0.01\cdot0.13\cdot0.1\cdot0.12\cdot0.02 = 2.8\cdot10^{-9}$  
$\displaystyle P(e_2)$ $\displaystyle =$ $\displaystyle 0.18\cdot0.07\cdot0.11\cdot0.21\cdot0.01\cdot0.13\cdot0.1\cdot0.01=3.8\cdot10^{-10}$  

Kertomalla priori ja käännöstodennäköisyys huomataan, että jälkimmäinen käännös on todennäköisempi:

$\displaystyle P(e_1)P(r\vert e_1)=0.063\cdot2.8\cdot10^{-9}=1.8\cdot10^{-10}$      
$\displaystyle P(e_2)P(r\vert e_2)=2.6\cdot10^{-10}$      

Huomattavaa on, että käännösmalli ei ota mitään kantaa sanajärjestykseen. Koska myöskään kielimalli (unigrammimalli) ei tätä tee, mallin mielestä sanajärjestyksellä ei ole mitään merkitystä. Jos mallilta kysytään todennäköisintä lausettta (ei testata eri vaihtoehtoja) huomataan, että todennäköisimpään lauseeseen ei voi tulla artikkeleja eikä sanaa ``into''. Tämä johtuu siitä, että niiden lisääminen ei muuta käännöstodennäköisyyttä, mutta tiputtaa aina kielimallitodennäköisyyttä. Kielimalli siis suosii muutenkin lyhyempiä lauseita. Kasvattamalla kielimallin konteksti trigrammiksi, saisi ehkä artikkelit ja sanajärjestyksen paremmin kohdalleen.

Yleisesti tällä menetelmällä tarvitaan heuristiikkaa valitsemaan käännökset, joita tutkitaan. Kaikkien vaihtoehtojen läpikäynti on käytännössä mahdotonta.


vsiivola@cis.hut.fi