Toinen kaava
![]() kertoo, että satunnainen sana on todennäköisyydellä
kertoo, että satunnainen sana on todennäköisyydellä ![]() kolmikirjaiminen ja todennäköisyydellä
kolmikirjaiminen ja todennäköisyydellä ![]() jotain muuta.
jotain muuta.
Todennäköisyys, että satunnainen sana on kolmikirjaiminen lyhenne
saadaan kertomalla
edellä annetut todennäköisyydet keskenään. Eli ensin katsotaan, kuinka
todennäköistä on, että sana on kolmikirjaiminen ja sitten vielä kuinka
todennäköistä on, että kolmikirjaiminen sana olisi lyhenne:
Sivuhuomautuksena sanottakoon, että annetut todennäköisyydet eivät varmaankan päde todelliselle englannin kielelle.
Jos pojat olisivat vain hieman ovelampia, he päättäisivät,, että
vain yksi heistä arvaa ja muut ovat hiljaa. Tällöinhän
voittotodennäköisyys olisi ![]() .
.
Muttu Pupu ei puhunut puppua. Jos tarkastelemme mahdollisia tuloksia,
löydämme vielä paremman strategian (taulukko 1). Kaikki
taulukon tapahtumat ovat yhtä todennäköisiä.
Huomaamme, että on vain kahdenlaisia tuloksia:
- 1)
- Kaikilla veljeksillä on samanvärinen hattu päässään
- 2)
- Yhdellä veljistä on erivärinen hattu kuin muilla.
Veljesten keksimä strategia kattoi tapaukset, jossa yhdellä veljellä
oli erivärinen hattu kuin muilla. Tässä tilanteessa pitää sen
veljen, joka näkee kaksi samanväristä hattua veikata omaa hattuaan
eriväriseksi. Ne jotka näkevät kaksi eriväristä hattua pitävät suunsa
kiinni. Tällä strategialla katetaan 6 kahdeksasta alkeistapauksesta,
ja saadaan voittotodennäköisyydeksi ![]() .
.
Kuinka paljon poikien kannattaisi maksaa peliin osallistumisesta ? Voittonahan oli yhteensä 1 euron arvoiset jätskit. Jos peliä pelattaisiin äärettömän monta kertaa, keskimääräinen voitto olisi
Kun peliä kuitenkin pelataan vain kerran, on hyvin subjektiivinen kysymys, miten paljon kannattaa sijoittaa. Jos pitää pelaamisesta, voi maksaa paljonkin ilman mitään toivoa voitosta (flipperi), toisaalta jos ei halua riskeerata säästöjään, ei ehkä kannata tarjota juuri mitään peliin osallistumisesta. Pojilla oli taskunpohjalle jäänyt 10 senttiä Sudenpentujen Käsikirjan uuden painoksen ostamisen jälkeen ja tämän he suostuivat asettamaan pelipanokseksi.
Nyt voimme laskea Bayesin kaavaan
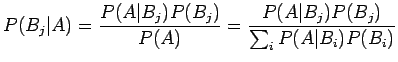 |
avulla todennäköisyyden, että laiteen väittäessä sanan perusmuodoksi ``siittää'' se on myös oikeassa.
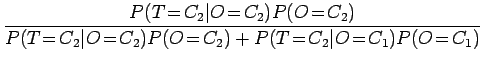 |
|||
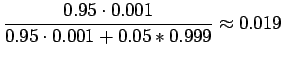 |
Sanoista, joiden perusmuodoksi laite on ehdottanut ``siittää'' vain joka viideskymmenes on oikein jäsennetty. Vaikka Åke olikin saanut ihan hyvät tunnistustulokset sinänsä, käytännön testejen jälkeen hän päätti romuttaa tunnistimensa ja ryhtyä jazz-muusikoksi.
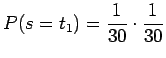 |
Tällaisia sanoja on 29 kappaletta.
Vastaavasti, tietyn kahden merkin pituisen sanan todennäköisyys on
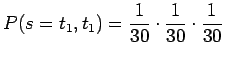 |
Tällaisia sanoja on
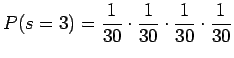 |
ja näitä sanoja on siis
Koska sanan esiintymistodennäköisyys on suoraan verrannollinen sen
odotettuun esiintymistiheyteen testiaineistossa, voimme tehdä kirjan
taulukon 1.3 kaltaisen taulukon suoraan laskemalla todennäköisyyksiä.
Koska samanpituiset sanat ovat yhtä todennäköisiä eikä niitä voi
asettaa yleisyysjärjestykseen, laskemme ![]() :n arvon vain yhdelle
samanpituisista sanoista. Tulokset on
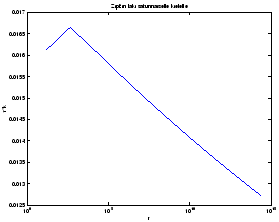
esitetty taulukossa 2 ja piirretty kuvaan 1.
:n arvon vain yhdelle
samanpituisista sanoista. Tulokset on
esitetty taulukossa 2 ja piirretty kuvaan 1.
| 15 | 1111 | 16111 |
| 450 | 37.04 | 16648 |
| 13064 | 1.235 | 16129 |
| 378900 | 0.0412 | 15593 |
| 1098800 | 0.00137 | 15073 |
| 318660000 | 0.0000457 | 14570 |
Huomataan, että satunnaisellakin kielellä
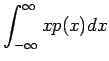 |
|||
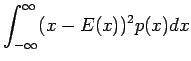 |
- a)
- Lasketaan odotusarvo yhden heiton silmäluvuksi. Noppa
laskeutuu jokaiselle 101:lle sivustaan yhtä todennäköisesti, eli
jokaisen tapahtuman todennäköisyys
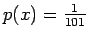 .
.
Odotusarvo:
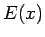

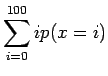

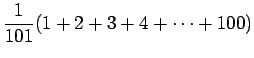

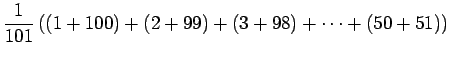

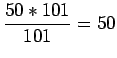
Varianssi voidaan laskea kaavalla:
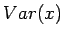

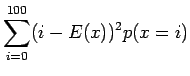

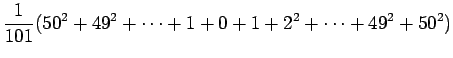

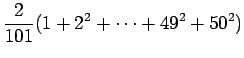
Nyt voimme käyttää avuksemme seuraava kaavaa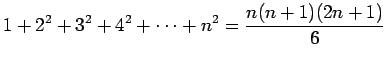
jolloin saamme tulokseksi
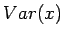

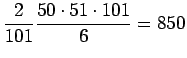
- b)
- Ratkaistaksemme tämän tehtävä, tarvitsemme muutamia
todennäköisyyslaskun peruskaavoja. Kaavat on tässä johdettu, mutta
niiden johtamisen osaaminen ei ole olennaista kurssin kannalta.
Riippumattomien satunnaismuuttujien summan oletusarvo
Olkonn satunnaismuuttujat x ja y riippumattomia. Lasketaan näiden satunnaismuuttujien summan oletusarvo.
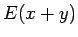

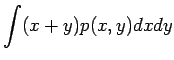

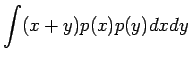

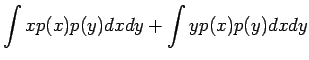

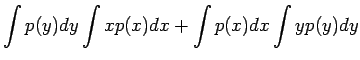

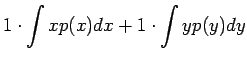

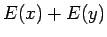
Vakiolla kerrotun satunnaismuuttujan varianssi
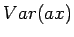

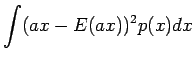

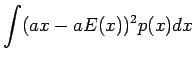

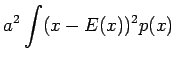

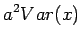
Riippumattomien satunnaismuuttujien summan varianssi
Olkoon satunnaismuuttujat x ja y riippumattomia. Lasketaan näiden satunnaismuuttujien summan varianssi.
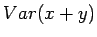

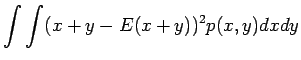

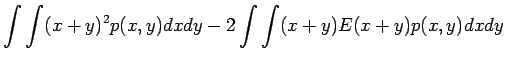
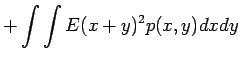

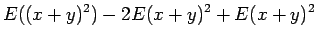

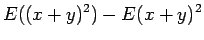

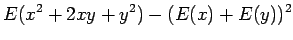

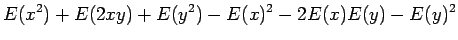

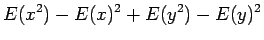
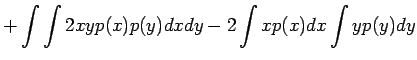

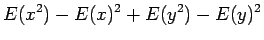

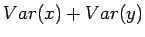
Tämän pakerruksen jälkeen päästään itse asiaan. Nyt halutaan laskea oletusarvo lauseelle
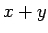 , missä
, missä 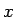 on ensimmäiseen heittoon
liittyvä satunnaismuuttuha ja
on ensimmäiseen heittoon
liittyvä satunnaismuuttuha ja 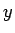 on toiseen heittoon liittyvä
satunnaismuuttuja.
on toiseen heittoon liittyvä
satunnaismuuttuja.
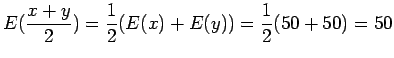
Huomaamme siis, että odotusarvo ei muutu. Entä miten käykään varianssin ?
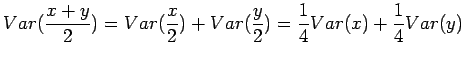
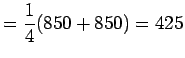
- c)
- Heitämme kymmentä noppaa, sovellamme edelle opittuja
tuloksia. Odotusarvo
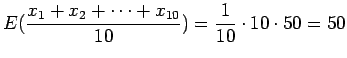
Varianssi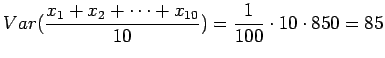
- d)
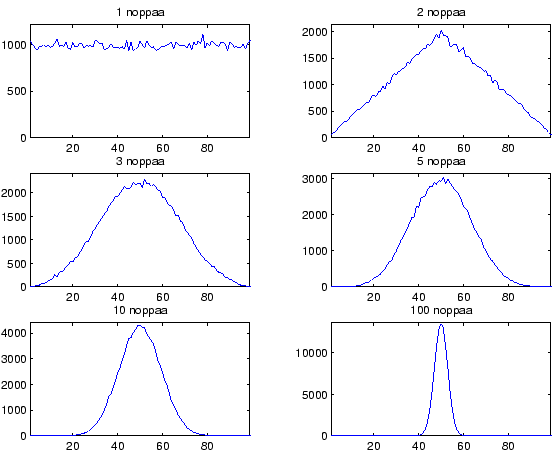
- Kun heitämme yhä useampaa noppaa, tarkentuu jakauma odotusarvon ympärille. Rajalla odotusarvo on 50 ja varianssi 0 eli saamme aina varmasti tulokseksi 50.
Odotusarvo ja varianssi eivät suinkaan kerro kaikkea jakaumasta. Kuvassa 2 on simuloitu matlabilla erilaisia määriä nopanheittoa. Huomaamme että jakauman muoto muuttuu, mitä useampaa nopaa heitetään. Muoto tulee lähemmäksi ja lähemmäksi normaalijakaumaa. Tämän takia useita luonnollisia ilmiöitä mallinnetaan normaalijakaumalla: Jos tulokseen vaikuttaa monta pientä satunnaista asiaa, tulos on normaalisti jakautunut. Tämä on myös hyvä tekosyy käyttää normaalijakaumaa, jolla saadaan laskut usein helppoon muotoon.
Formaalimpi todistelu siitä, että jakauma lähestyy normaalijakaumaa löytyy http:// mathworld.wolfram.com/CentralLimitTheorem.html