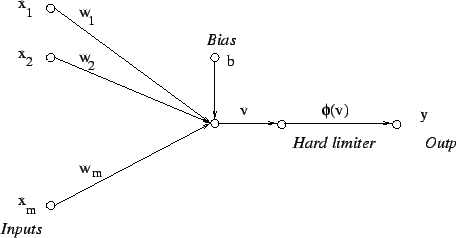
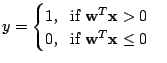 |
where
- not
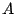 or
or
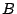
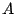 and
and 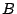
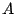 nor
nor 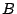
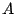 nand
nand 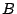
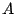 xor
xor 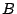 .
.
where
where
Observation vector
![]() belongs to class
belongs to class
![]() if the output
if the output ![]() where
where ![]() is a threshold;
is a threshold;
otherwise,
![]() belongs to class
belongs to class
![]()
Show that the decision boundary so constructed is a hyperplane.
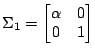 and and 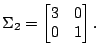 |
Plot the distributions and determine the optimal Bayesian decision surface for