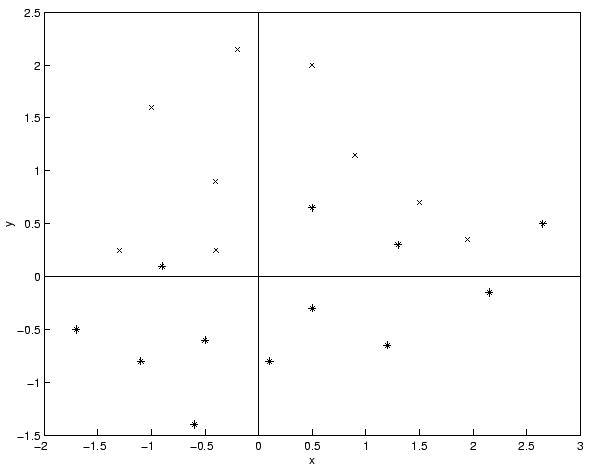
where
- The simple form of Hebb's rule described by
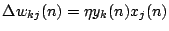
assuming the learning rate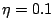 .
.
- The covariance rule described by
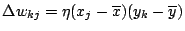
assuming that the time-averaged values of the presynaptic signal and postsynaptic signal are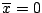 and
and
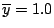 ,
respectively.
,
respectively.
What is the condition that would have to be satisfied for neuron
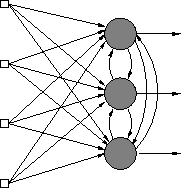 |