Tik-61.183 Special course on information technology III
Randomized algorithmsSpring 2000
Heikki Mannila
Exercises 2, due February 16, 2000
- 1.
- Assume we have a file containing N records, where N is so
large that we cannot keep all of the file in memory at one time.
We wish to select a random subset of n records from the file.
We will use the following algorithm:
Set t:=0, m:=0. Repeat until m=n: Generate a random number U, uniformly distributed between 0 and 1. If U<(n-m)/(N-t), then Add the next record from the file into the subset. Set m:=m+1. Else Skip the next record. Set t:=t+1.Prove that the algorithm doesn't try to read more than N records from the file. Prove that each of the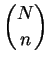 subsets is equally likely to be selected.
subsets is equally likely to be selected.
- 2.
- Let p(x,y) be the probability that exactly x records are
selected from among the first y by the previous algorithm.
Show that
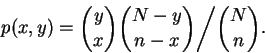
- 3.
- What is the expected value of t when the algorithm
terminates? What is the variance?
- 4.
- Devise an algorithm to select a random permutation of n objects using O(n) random numbers. Each permutation should be
equally likely.
http://www.cis.hut.fi/Opinnot/T-61.183/k2000/exercises/2/exercise2.shtml
jkseppan@mail.cis.hut.fi
Wednesday, 09-Feb-2000 20:43:29 EET