Tik-61.183 Special course on information technology III

Exercises 1, due February 9, 2000

1.

The variance D²(X) of a random variable X is the expectation of the random variable (X-E(X))², i.e., D²(X) = E((X-E(X))²). The variance is also denoted by 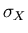, or by var[X]. Show that D²(X) = E(X²) - (E(X))².

2.

Let X(n) be the number of tails obtained when flipping a fair coin n times. What is E(X(n))? What is D²(X(n))?

3.

Let X(n,p) be the number of heads obtained when flipping a biased coin (probability of head = p) n times. Compute E(X(n,p)) and D²(X(n,p)).

4.

Find Markov's inequality from a textbook and give an informal justification of it. State Chebyshev's inequality.

5.

Approximate (either analytically or by simulation) the probability of the following event: ``When flipping a fair coin 1000 times, the number of heads is less than 450''.