Probability density estimation

 

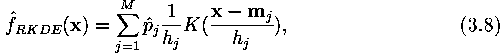
Since the distribution of the weight vectors of the SOM approximates that of the training data, the SOM can be utilized in estimating the probability density function (PDF) of a data set. The estimation can be done using e.g. the reduced kernel density estimation (RKDE) [10]:

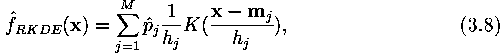
where M is the number of neurons in the map, K is a kernel function and the weights and the smoothing parameters are estimated from the data. The batch version of the algorithm proceeds as follows:

1. Train the kernel centers using the SOM.
2. Calculate the weights , where is the number of samples in the Voronoi region of the reference vector .
3. Calculate a single smoothing parameter h, or perhaps different for each kernel. This can be done e.g. by computing the distance between and its nearest model vector, setting , and optimizing as the Breiman-Meisel-Purcell estimator.