The first proposed criteria to measure the topology preservation of the SOM was the topographic product [1]. It tests the similarity of neighborhood on the map and in the input space. However, it has been pointed out that the topographic product does not work except for linear submanifolds because it cannot distinguish between a correct folding due to a folded data manifold from a folding due to a topological mismatch between the data manifold and the SOM lattice. In its stead Villmann et al. [42] proposed topographic function which measures the number of map units having adjacent receptive fields in the input space, but a distance greater than k on the grid:
where 
is the location of unit i on the grid and 
is the connectivity matrix; a binary matrix with element (i,j) equal
to one only if map units i and j are two closest BMUs of any input
vector 
from the training set. A problem with
this measure is how to compare two different topographic functions.
A simpler method was proposed by Kiviluoto [20]. He
calculated topographic error as the proportion of sample vectors for
which two best matching weight vectors are not in adjacent
units:
where 
if the first and second BMUs of 
are not adjacent units, otherwise zero. The advantage of this measure
is that the results are directly comparable between different mappings and
even mappings of different data sets. It is also very easy to interpret.
Another branch of methods are those that do not use a data set at all. These methods do not measure the topology preservation property of the map but rather its local smoothness. One such method was proposed by Hämäläinen [9]. His measure of disorder requires that the distance between each unit i and its neighbors j is smaller than the distance between unit i and the neighbors k of the respective unit j:
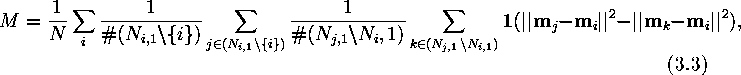
where 
is the 1-neighborhood of unit i, 
is its cardinality, N is the total number of units on the map and
is the step function.
