Enhancing SOM based data visualization

Introduction

The Self-Organizing Map (SOM) [5] is a neural network algorithm which is based on unsupervised learning and combines the tasks of vector quantization and data projection. The SOM has proven to be a valuable tool in data mining and knowledge discovery with applications in full-text and financial data analysis [3]. The SOM has also been successfully applied in various engineering applications covering, for instance, areas like pattern recognition, image analysis, process monitoring and control, and fault diagnosis [6], [8].

The SOM consists of a set of neurons organized on a regular, usually 1- or 2-dimensional grid. Higher dimensional grids can but they are not generally used since their visualization is problematic. Each neuron $i$ on the grid corresponds to a location in the input space m_i = [m_i1,...,m_in]. The SOM acts as a vector quantizer algorithm, like k-means [1]. The important distinction is that on each update cycle along with the selected neuron also its neighbors, neighboring units on the grid, are updated. This way the SOM orders the neurons so that similar input samples are projected onto nearby neurons on the map. During the iterative training, the SOM behaves like an elastic net that folds onto the "cloud" formed by input data.

There are many ways in which the SOM can be used for data visualization and exploration. In this paper, we propose new ways to enhance the visualization in the areas of detecting component correlations, clustering structure and novelty of data vectors.

Correlations

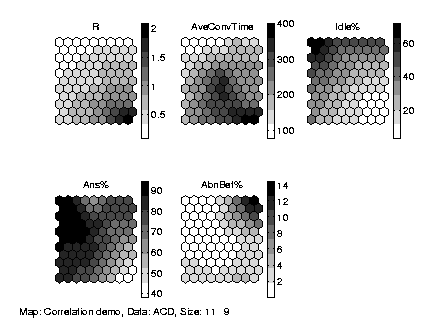
The SOM is a useful tool in "correlation hunting", that is, in inspecting the possible correlations between vector components in the input data, which may be for example process parameters. In practice the SOM is sliced to component planes. Each plane represents the value of one component in each node of the SOM using gray-level or colour representation, as shown in Fig.1. By comparing these planes even partial correlations may be found.

Figure 1. Component planes of a SOM. R: phone call traffic intensity, AveConvTime: average call length, Idle%: ratio of idle agents, Ans%: ratio of calls answered, AbnBef%: ratio of calls which abandoned before a target time. Bottom right figure: coding of the map units with rectangles of different size and colour. See Fig.1. Click on figures to get a larger version.

However, an accurate comparison of colour coded values on the planes is difficult or even impossible. A more detailed comparison between two components can be made using the familiar two dimensional function plot. Of course, this can be done without using the SOM as an intermediate tool, but the SOM offers benefits over this simplistic approach. Firstly, the SOM averages data and thus removes noise. Secondly and more importantly, the SOM allows the inspection of correlations even if they differ in different parts of the data space. In Fig.2a it can be seen that there are clearly two modes by which the two components depend on each other.

In addition, these correlations are clearly localized by the SOM. In Fig.2 the spatial coding has been done using a smooth colouring for the map grid (in the paper, which is B/W, the coding is based on size and shade of gray). Essentially a point on the function plot may be associated to a map unit and thus to other visualizations. This kind of linking by a continuous colour coding can be used to link different kinds of SOM visualizations, for example Sammon's projection of the map grid (see Fig. 2c and 2d). This may be useful while evaluating the relations between different regions of a projection, e.g. in tracking process state transitions using a trajectory. A very useful colour coding results by assigning the colours according to the cluster structure of the map, as proposed by Kaski et al. [4].

(a) Ratio of idle agents vs. answering percent	(b) Ratio of idle agents vs. quickly abandoned calls	(c) Spatial coding for the grid: gray level indicates x-axis and size y-axis.
Figures (a) and (b) present two pairs of vector components of the SOM in Fig.1 as function plots. The data is from a help desk queuing system. Figure (c) shows the size--gray level spatial coding which links the map grid in Fig.1 and the function plots in (a) and (b). Click on figures to get a larger version.

Clusters

Clusters of the SOM are typically visualized using a matrix of distances between neighboring map units, like the U-matrix [9]. Another way to approach clusters is to observe the overall shape of the map. So far the primary technique to visualize the shape of the map has been to project the map units using some projection technique, such as Sammon's projection [7] or the CCA [2]. When the projections of neighboring units are connected with lines this results is a net-like presentation, as shown in Fig.3.

(a) 2D projection	(b) 3D projection
(c) Colour coding	(d) 3D projection
Figure 3. Sammon's projections of a SOM. (a) 2D projection, (b) 3D projection, (c) a component plane of the map which is used for colour coding the map units, (d) the 3D projection seen from from another angle with colour coding. The data is from a database having information of the pulp and paper mills of the world. Its characteristics include very high dimension (75) combined with many overlapping clusters. Click on figures to get a larger version.

For the purpose of clustering, there are however several drawbacks. The foremost of these drawbacks has nothing to do with SOM. Usually only 1D or 2D projections are used because their visualization is simple. However, the low projection dimension is obviously a huge restriction. We strongly suggest that when the tools at hand allow it, 3D projections should be used. In Fig.3 both a 2D projection of a map, and two views of a 3D projection are shown. It can be clearly seen that the 2D projection has folded, and is thus inadequate for the projection task. The 3D projection, on the other hand, fares much better.

While dimension of 3 is not very big either, it is the largest that human beings can easily grasp, and it is also becoming feasible with today's technology. A drawback of 3D projections is of course that they cannot be effectively used in 2D media, such as on paper, because 3D visualizations need to be interactively rotatable. However, 3D visualizations can be easily implemented for example using VRML.

The second drawback is that SOM interpolates between map units inserting units between clusters, thus obscuring cluster borders. This can be bypassed by emphasizing the visualization of the map units according to the number of "hits" they recieve from the teaching data set.

A third drawback has to do with high-dimensional data. In high dimensions the data always tend to be sparce due to the curse of dimensionality, and this makes the work of projection algorithms hard. The SOM, on the other hand, still finds clusters from the data since on the grid the location of neurons depends only on their nearest neighbors, not on all available data. This advantage can be transferred to the projection by replacing each projected data vector by a weighted average of the data vector and its Best-Matching Unit (BMU; map unit closest to the data vector in the input space) on the map, i.e. moving the data vectors towards the respective cluster centers. See Fig.4.

Figure 4. Sammon's projection of the original 75-dimensional pulp and paper mill data (the same as in Fig.3). (b) The projection of a modified data set: each data vector was replaced by a weighted average of the data vector and its BMU on the map. Click on figures to get a larger version.

Novelty detection

Many times the most interesting thing about a map is not the map itself but how it corresponds to actual data. What is the location of a given data vector on the map? This is typically depicted by the BMU of the data vector. By combining the BMUs of a whole set of data vectors, a data histogram is obtained where the value of the histogram tells the number of times each map unit was the BMU.

The problem with simply pointing out the BMU is that it tells nothing of the precision of the match. Does the data vector "belong" to the map, or is it novel vector from entirely another distribution not covered by the map? An indication of the novelty is the quantization error between the data vector and its BMU: q_i = |x_i - m_BMU(i)|. If the quantization error is large compared to the local accuracy of the map unit, the data vector is probably from a different distribution than the original training data.

This information can be added to the visualization by taking the z-axis into use, as in Fig.5. Each data vector is then shown as a bar, the height of which is proportional to the quantization error normalized by the local accuracy. Local accuracy can be approximated for example by the average distance of the map unit to its neighbors.

Figure 5. Novelty visualization of a set of data vectors. Each bar denotes one data vector. The position of the bar is the BMU of the data vector plus small random scatter so that individual bars can be separated from each other. The height of the bar is proportional to the normalized quantization error of the data vector. On the bottom is the U-matrix of the SOM. The grid shows the height which corresponds to the local accuracy. Bars which are much higher than the grid are suspect of being novel vectors. The data are measurements from the central processor of a computer network. Click on figures to get a larger version.

Conclusion

The SOM is a versatile tool for data mining which combines the tasks and advantages of vector quantization and data projection. The visualization methods presented in this paper offer efficient ways to enhance the visualization of the SOM in data exploration. The tasks in exploratory data visualization are very heterogeneous, but as the proposed principles are simple, they can be easily modified to meet the needs of the task. Future work is still needed to enable the methods to automatically take into account the properties of the underlying data.

Acknowledgments

References

1. C.M.Bishop.
   Neural Networks for Pattern recognition.
   Oxford University Press, 1995.
2. P.Demartines and J.Hérault.
   Curvilinear component analysis: a self-organizing neural network for nonlinear mapping of data sets.
   IEEE Transactions on Neural Networks, 1997.
3. S.Kaski.
   Data Exploration Using Self-Organizing Maps.
   PhD thesis, Helsinki University of Technology, 1997.
4. S.Kaski, T.Kohonen, and J.Venna.
   Visual explorations in Finance using Self-Organizing Maps, chapter Tips for SOM Processing and Colorcoding of Maps.
   Springer-Verlag, London, 1998.
   In press.
5. T.Kohonen.
   Self-Organizing Maps.
   Springer, Berlin, Heidelberg, 1995.
6. T.Kohonen, E.Oja, O.Simula, A.Visa, and J.Kangas.
   Engineering applications of the self-organizing map.
   Proceedings of the IEEE, 84(10):27 pages, October 1996.
7. J.W.Sammon, Jr.
   A nonlinear mapping for data structure analysis.
   IEEE Transactions on Computers, C-18(5):401-409, May 1969.
8. O.Simula and J.Kangas.
   Neural Networks for Chemical Engineers, volume 6 of Computer-Aided Chemical Engineering, chapter 14, Process monitoring and visualization using self-organizing maps.
   Elsevier, Amsterdam, 1995.
9. A.Ultsch and H.P. Siemon.
   Kohonen's self organizing feature maps for exploratory data analysis.
   In Proc. INNC'90, Int. Neural Network Conf., pages 305-308, Dordrecht, Netherlands, 1990. Kluwer.