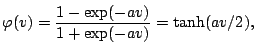Tik-61.261 Principles of Neural Computing
Raivio, Venna

Exercise 1

1. An odd sigmoid function is defined by

   $$\varphi(v)=\frac{1-\exp(-av)}{1+\exp(-av)}=\tanh(av/2),$$

   
   
   where $\tanh$ denotes a hyperbolic tangent. The limiting values of this second sigmoid function are $-1$ and $+1$. Show that the derivate of $\varphi(v)$ with respect to $v$ is given by

   $$\frac{d\varphi}{dv}=\frac{a}{2}(1-\varphi^2(v)).$$

   
   
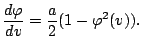   What is the value of this derivate at the origin? Suppose that the slope parameter $a$ is made infinitely large. What is the resulting form of $\varphi(v)$?

2. 1. Show that the McCulloch-Pitts formal model of a neuron may be approximated by a sigmoidal neuron (i.e., neuron using a sigmoid activation function with large synaptic weights).
   2. Show that a linear neuron may be approximated by a sigmoidal neuron with small synaptic weights.

3. Construct a fully recurrent network with 5 neurons, but with no self-feedback.

4. Consider a multilayer feedforward network, all the neurons of which operate in their linear regions. Justify the statement that such a network is equivalent to a single-layer feedforward network.

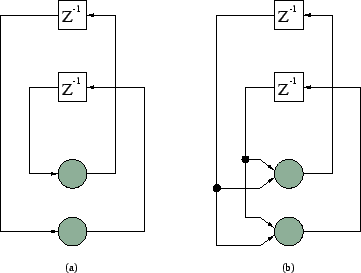
5. 1. Figure 1(a) shows the signal-flow graph of a recurrent network made up of two neurons. Write the nonlinear difference equation that defines the evolution of 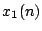$x_1(n)$ or that of 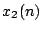$x_2(n)$. These two variables define the outputs of the top and bottom neurons, respectively. What is the order of this equation?
   2. Figure 1(b) shows the signal-flow graph of a recurrent network consisting of two neurons with self-feedback. Write the coupled system of two first-order nonlinear difference equations that describe the operation of the system.

Figure 1: The signal-flow graphs of the two recurrent networks.