max 3p
| (a) | Assuming that all codewords are the
same length, find the minimum length required to provide codewords for
all sequences with three or fewer ones.
You need to compute how many sequences have 0-3 ones. This number is 1+100+100*99/2+100*99*98/6, which is less than 2^18. Therefore 18 bits is enough. |
| (b) | Calculate the probability of observing
a source sequence for which no codeword has been assigned.
This is the probability of a sequence, which has 4 or more ones. This equals one minus the probability of a sequence with 0-3 ones, i.e, 1 - (0.995)^100 - 100*0.005*(0.995)^99 - 100*99/2*(0.005)^2(0.995)^98 - 100*99*98/6*(0.005)^3(0.995)^97, approximately 1.7*10^(-3). |
| (c) | Use Chebyshev's inequality to bound
the probability of observing a source sequence for which no codeword
has been assigned. Compare this bound with the actual probability
computed in part (b).
We use the Chebyshev inequality P(t>=a)<=E[t]/a. If we denote t as the number of ones in the sequence, we get P(t>=4)<=E[t]/4=0.005*100/4=0.5/4=0.125 This is much larger than the result of b). The other Chebyshev inequality can also be used, resulting in P(t>=4)<=0.0406... We omit the details. |
max 2p
We only need to look at the difference between the entropies of the mentioned probability distributions. Define f(p)=-p log p. Then the difference is
2*f(pi+pj)-f(pi)-f(pj)
which we need to show to be less than or equal to zero:
f((pi+pj)/2)<= 1/2 (f(pi)+f(pj))
This follows if f is convex. Since df/dp=log p+1, it follows that d^2 f/dp^2=1/p>0 when p>0, hence f is convex.
We need to define "more uniform". This is conveniently done using Kullback-Leibler divergence D(p,u) where u is the uniform distribution with m discrete probabilities 1/m. If D(p,u)>D(q,u), it means that q is "more uniform" than p. Since
D(q,u)=sumi qi log (qi/(1/m))=-H(q)- sumi qi log m^-1=-H(q)+log m
the inequality turns out to be -H(p)>-H(q) or H(p)<H(q) as desired.
max 2p
Answer omitted, the code varies depending whether you include spaces or not etc...
max 2p
Each image has n=256*256*8 bits, then there are 2^n possible images. Denote l=n-20, which is the largest codelength of an image that fulfills the requirement given in the problem. Then Kraft-inequality gives an upper bound k as k*2^(-l)<=1 or k=2^l=2^(n-20). This is an upper bound, since shorter codelengths m<l would correspond to larger terms 2^(-m) in the Kraft inequality.
To compare k with 2^n, divide k/2^n=2^(n-20)/2^n=2^(-20), which is approximately 0.000095 percent. So compression is difficult!
max 2p
The problem is otherwise identical to the one solved in MacKay's book in section 4.2.4, except that the prior is different. The solution is (Na + 1/2) / (Na + Nb + 1).
max 2p
Some reasons: the noisy channel coding theorem assumes, that the
code is a block code and the block length can be chosen arbitrarily
large. This is not reasonable in practice.
The channel capacity is assumed to be constant and known. This does
not always hold in practice.
max 2p
- E(|x|)=1
- Absolute value |x| is at most one
- E(x^2)=1
The task is to maximize an integral over -p(x)log(p(x)) under constraints. The constraints can be expressed by integrals over p(x)f(x) = constant. The first constraint is that p(x) has to integrate to unity (f(x) = 1) and the next constraint is the one given in the problem. In the first problem f(x) = |x| and in the third problem f(x) = x^2. In the second problem the domain of x is [-1,1] but there are no other constraints.
Using the method of Lagrange multipliers one can show that a general form of the solution is exp(c1f1(x) + c2f2(x) + ...), where ci are the Lagrange multipliers, one for each constraint.
The solutions are:
- p(x) = exp(-|x|)/2 (Laplace distribution), entropy ln 2e.
- p(x) = 1/2 (even distribution), entropy ln 2.
- p(x) = exp(-x^2 / 2)/sqrt(2 pi) (normal distribution), entropy 1/2 ln 2 pi e.
max 2p
Use the conjugate priors and add them into the posterior probability according to Bayes' theorem. Details omitted here.
max 2p
The solution is obtained as explained in the supplement to the
problem. It is 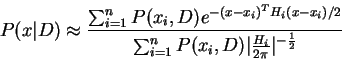 .
.
max 2p
You need to use heavy approximations. First, ignore everything but
visual information; other sensory information should be a small
fragment of the visual information. Estimate your lifetime, say, in
seconds. Use only 1 significant digit:
30yrs*400days*20hrs*60minutes*60seconds
is about 900 million seconds. The eye has about 6-7 million cones
(highly sensitive to light intensity) and is able to distinguihs
about 1 million levels of intensity. Multiply 6 billion by 2 (two
eyes) and by 3 (we see colors too). 36 billion times 900 million is
3*10^22 bits. Since we sleep etc., let's say our sensory experience
is 10^22 bits. Oh, lets multiply by 20 since we do notice visual
changes happening up to that rate. So the final number is
2*10^23 bits.
The capacity of the brain is 2*10^14 bits, far less
than our sensory experience.
Don't worry, your brain did not fill up when you were 3*10^(-8) years
old. Instead, the sensory experience we just computed is *raw* data.
If I look at a peaceful scenery for 1 hour, my brain does not probably
store the full data of what I see 20 times per second. Some data is
ignored and the rest is represented, i.e. coded in the brain.
The representation is probably used in coding future sensory data;
what happens in the brain when I start to look at the scenery is
different than what happens after 1 hour of looking.
max 2p
The ensemble distribution implicitly assumed in the MML method is a hyper-box whose sides have lengths ei. Let us denote this distribution by Q(w). The coding length in MML is L(parameters) + L(data | parameters) = - log P(w1)e1 - log P(w2)e2 - ... - EQ{log P(D | w)}.
The bits-back argument assumes that the sender picks the parameters w from distribution Q(w) and encodes them with an accuracy approaching infinity (ei -> 0). This makes the terms -log P(wi)ei infinite, but an infinite number of bits are got back also, since the sender can embed a secondary message in the choise of the parameters. The expected total number of bits used in coding is L(parameters) + L(data | parameters) - bits back = - EQ{log P(w)} - EQ{log P(D | w) } + EQ{log Q(w)}.
Choosing the Q(w) to be the same as in MML yields identical coding length since - EQ{log P(w)} + EQ{log Q(w)} = - log P(w1)e1 - log P(w2)e2 - ...
In the MML scheme the coding cost of the discretation accuracies ei is neglected, but in the bits-back scheme the sender and the receiver can agree in advance on arbitrarily small discretation intervals ei.
max 1p
Only the sign of the constant n is significant, since the activation is a linear combination of the weights and the constant appears as a multiplier of the activation. The state is updated using a step function of the activation, where only the *sign* of the activation is significant.
max 2p
Straightforward but tedious calculation, omitted here.
max 2p
Straightforward but tedious calculation, omitted here.
max 2p
Exercise 13.3 in the book, page 276.
Straightforward calculation, omitted here.