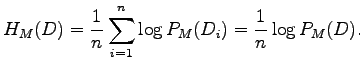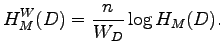- a)
- Alustetaan hila siten, että lähtötila on aina
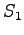 . Merkitään ylös
vain nollasta poikkeavat todennäköisyysarvot.
. Merkitään ylös
vain nollasta poikkeavat todennäköisyysarvot.
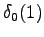

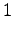
Ensimmäinen havainto
Aloitustilasta pääsee vain toiseen ja neljänteen tilaan, joten lasketaan niiden todennäköisyydet:
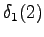

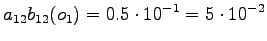
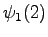

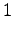
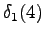


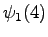

Toinen havainto
Toisesta tilasta päästään vain kolmanteen ja neljännestä vain viidenteen tilaan, joten vieläkään ei tarvita reittivalintoja.
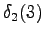

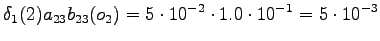
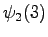

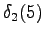

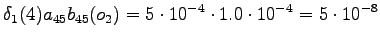
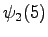

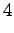
Tässä vaiheessa pitää kuitenkin huomata, että tiloista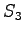 ja
ja 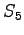 pääsee
nollasiirtymällä aloitustilaan. Toisen havainnon jälkeen voidaan siis päätyä
myös sinne. Lasketaan tilaan tulevista reiteistä todennäköisempi:
pääsee
nollasiirtymällä aloitustilaan. Toisen havainnon jälkeen voidaan siis päätyä
myös sinne. Lasketaan tilaan tulevista reiteistä todennäköisempi:
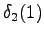

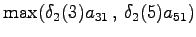

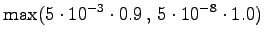

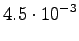
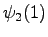

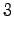
Kolmas havainto
Nyt mahdollisia ovat siirtymät tilasta
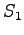 tilaan
tilaan 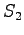 tai
tai 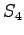 sekä
tilasta
sekä
tilasta 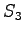 tilaan
tilaan 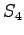 .
.
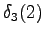

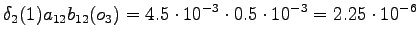
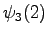

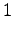
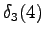

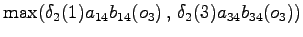

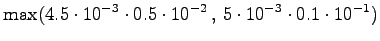

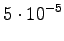
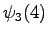

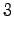
Neljäs havainto
Jälleen toisesta tilasta päästään vain kolmanteen ja neljännestä vain viidenteen tilaan.
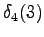

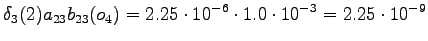
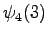

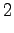
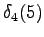

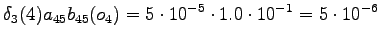
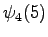

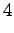
Lopetus
Lopuksi piti päästä takaisin tilaan
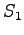 , mikä onnistuu nollasiirtymällä.
Reittivaihtoehtoja on kaksi:
, mikä onnistuu nollasiirtymällä.
Reittivaihtoehtoja on kaksi:
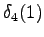

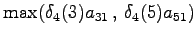

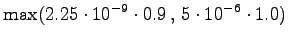

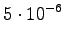
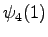

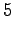
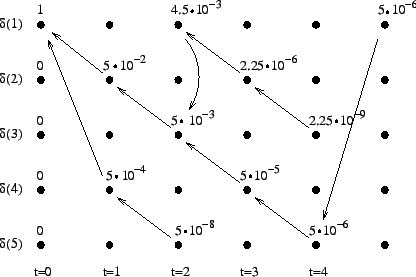
Laskettu hila on kuvassa 1. Palaamalla lopusta alkuun saadaan todennäköisin tilasekvenssi
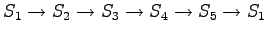 . Tämä vastaa
sanaa ``jaon''.
. Tämä vastaa
sanaa ``jaon''.
- b)
- Nyt pitää ottaa huomioon myös kielimallin antamat
todennäköisyydet. Lasketaan todennäköisyysarvot ehdollisina mahdollisille
eri sanavaihtoehdoille
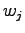 :
:
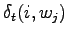 . Kielimallitodennäköisyys
kerrotaan mukaan aina kun sanan valinta tehdään. Kuljettaessa uudestaan
aloitustilan kautta valinnat pitää ottaa huomioon käyttämällä
bigrammitodennäköisyyksiä. Tämän jälkeen ne voidaan tyhjentää, koska
kielimalli ei tarvitse pidempiä historioita.
. Kielimallitodennäköisyys
kerrotaan mukaan aina kun sanan valinta tehdään. Kuljettaessa uudestaan
aloitustilan kautta valinnat pitää ottaa huomioon käyttämällä
bigrammitodennäköisyyksiä. Tämän jälkeen ne voidaan tyhjentää, koska
kielimalli ei tarvitse pidempiä historioita.
Alustetaan hila samoin kuin a)-kohdassa. Tässä vaiheessa ei ole vielä sanavalintoja.
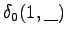

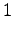
Ensimmäinen havainto
Aloitustilasta pääsee toiseen ja neljänteen tilaan. Toinen tila voi päätyä sanaan ``ja'' tai ``jaon'', joten kumpikin vaihtoehto pitää laskea erikseen.
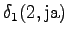

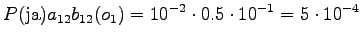
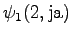

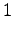
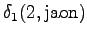

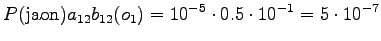
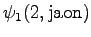

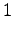
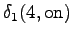

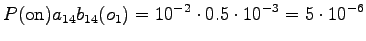
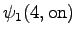

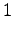
Toinen havainto
Toisesta tilasta päästään vain kolmanteen ja neljännestä vain viidenteen tilaan. Lisäksi kummastakin pääsee nollasiirtymällä ensimmäiseen tilaan. Tämä voidaan luonnollisesti tehdä vain sanoille jotka ovat käsitelty loppuun.
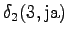

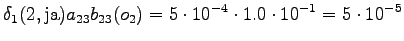
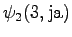

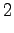
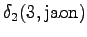

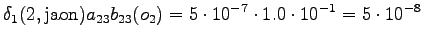
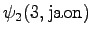

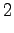
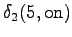

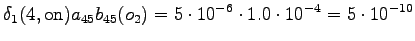
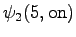

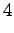
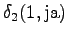

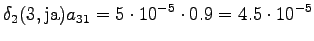
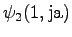

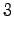
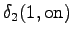

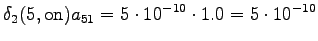
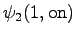

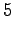
Kolmas havainto
Mahdollisia ovat siirtymät tilasta
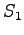 tilaan
tilaan 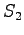 tai
tai 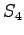 sekä
tilasta
sekä
tilasta 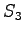 tilaan
tilaan 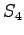 . Tilasta
. Tilasta 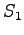 lähtevät siirtymät aloittavat
uuden sanan, joten otamme kielimallitodennäköisyydet huomioon. Lisäksi
pitää huomioida että tilassa
lähtevät siirtymät aloittavat
uuden sanan, joten otamme kielimallitodennäköisyydet huomioon. Lisäksi
pitää huomioida että tilassa 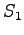 oli kaksi eri sanavaihtoehtoa,
joista nyt voidaan valita todennäköisempi.
oli kaksi eri sanavaihtoehtoa,
joista nyt voidaan valita todennäköisempi.
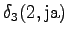

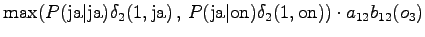

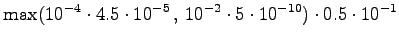

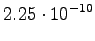
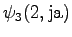

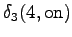

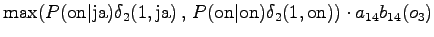

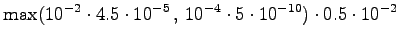

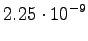
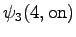

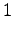
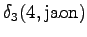

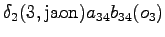

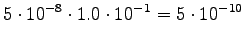
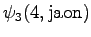

Neljäs havainto
Toisesta tilasta päästään vain kolmanteen ja neljännestä vain viidenteen tilaan. Kummastakin päästään vielä nollasiirtymällä ensimmäiseen tilaan.
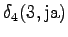

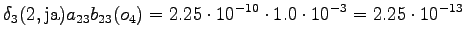
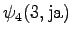

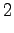
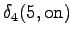

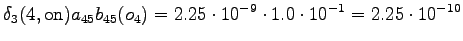
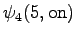

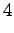
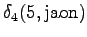

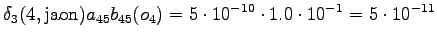
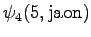

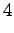
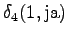

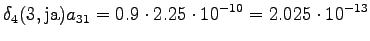
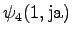

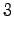
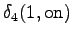

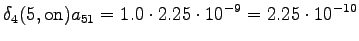
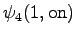

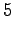
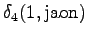

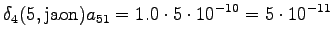
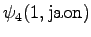

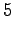
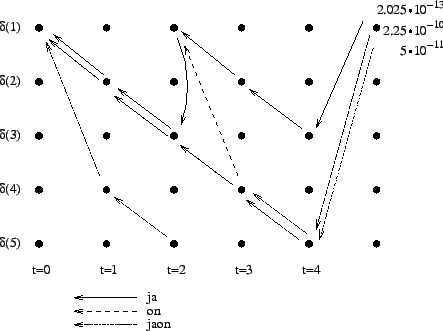
Laskettu hila on kuvassa 2. Eri sanavaihtoehdot on piirretty kuvaan erilaisilla nuolilla. Kolmesta lopetustilaan päätyneestä polusta todennäköisin on
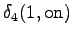 . Palaamalla siitä taaksepäin
saadaan todennäköisin tilasekvenssi
. Palaamalla siitä taaksepäin
saadaan todennäköisin tilasekvenssi
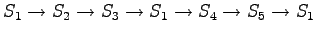 .
Nyt todennäköisimmäksi saatiin siis kahden sanan sekvenssi, ``ja on''.
.
Nyt todennäköisimmäksi saatiin siis kahden sanan sekvenssi, ``ja on''.
Sen sijaan voimme laskea malleille entropiat sanaa kohti.
Risti-entropia testidatalle ![]() voitiin laskea
voitiin laskea
Jos yksiköiden määrän
Tiedämme luvut
Muutetaan annetut entropiat sanakohtaisiksi:
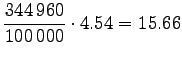 |
|||
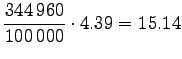 |
|||
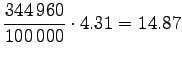 |
|||
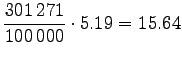 |
|||
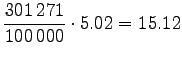 |
|||
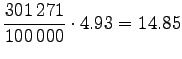 |
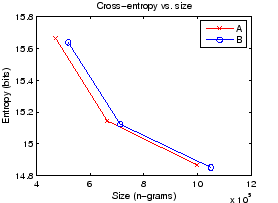
Pilkonnan B entropiat ovat siis kaikissa kokoluokissa hieman parempi kuin pilkonnan A. Pitää kuitenkin ottaa huomioon myös mallien koot, jotka pilkonnalla B olivat kauttaaltaan suurempia. Tulosten vertailu on helpointa piirtämällä kuvaaja, jossa tulokset on esitetty koko-entropia -koordinaatistossa. Tämä on tehty kuvassa 3.
Pilkonnan A mittauspisteitä yhdistävä murtoviiva on joka paikassa B:n viivasta katsottuna vasemmalla puolella. Pilkonta A näyttää siis antavan hieman parempia tuloksia kuin B suhteessa kielimallien kokoihin.
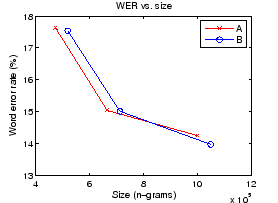
Katsotaan seuraavaksi tunnistustuloksia. Ne on laskettu suoraan sanoja kohti, joten normalisointeja ei tarvita. Mallin koko vs. sanavirhe -kuvaaja on esitetty kuvassa 4. Siitä nähdään, että tulokset isoilla ja pienillä malleilla menevät ristiin: A on parempi pienillä malleilla, mutta B ohittaa sen kun koot kasvavat yli 900000 n-grammin.
Näyttää kohtuullisen selvältä, että pilkontaa A käyttävät mallit ovat parempia jos mallin koko on pieni. Suuremmilla malleilla tulokset ovat melko lähellä toisiaan. Lisäksi toiminnasta malleilla joiden koot ovat selvästi alle puoli miljoonaa, tai selvästi yli miljoonan, nämä tulokset eivät kerro mitään. Luotettavammat tulokset vaatisivat lisää mittauspisteitä sekä lukujen tilastollisten merkittävyyksien testaamista (esim. Wilcoxon signed-rank test).