Toinen kaava
![]() kertoo, että satunnainen sana on todennäköisyydellä
kertoo, että satunnainen sana on todennäköisyydellä ![]() kolmikirjaiminen ja todennäköisyydellä
kolmikirjaiminen ja todennäköisyydellä ![]() jotain muuta.
jotain muuta.
Todennäköisyys, että satunnainen sana on kolmikirjaiminen lyhenne
saadaan kertomalla
edellä annetut todennäköisyydet keskenään. Eli ensin katsotaan, kuinka
todennäköistä on, että sana on kolmikirjaiminen ja sitten vielä kuinka
todennäköistä on, että kolmikirjaiminen sana olisi lyhenne:
Sivuhuomautuksena sanottakoon, että annetut todennäköisyydet eivät varmaankan päde todelliselle englannin kielelle.
Nyt voimme laskea Bayesin kaavan
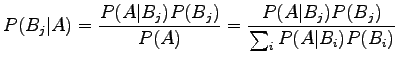 |
avulla todennäköisyyden, että laiteen väittäessä sanan perusmuodoksi ``siittää'' se on myös oikeassa.
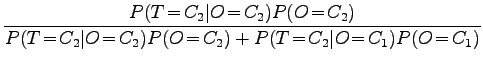 |
|||
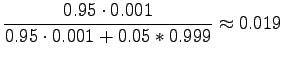 |
Sanoista, joiden perusmuodoksi laite on ehdottanut ``siittää'' vain joka viideskymmenes on oikein jäsennetty. Vaikka Åke olikin saanut ihan hyvät tunnistustulokset sinänsä, käytännön testejen jälkeen hän päätti romuttaa tunnistimensa ja ryhtyä jazz-muusikoksi.
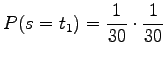 |
Tällaisia sanoja on 29 kappaletta.
Vastaavasti, tietyn kahden merkin pituisen sanan todennäköisyys on
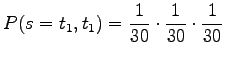 |
Tällaisia sanoja on
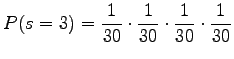 |
ja näitä sanoja on siis
Koska sanan esiintymistodennäköisyys on suoraan verrannollinen sen
odotettuun esiintymistiheyteen testiaineistossa, voimme tehdä kirjan
taulukon 1.3 kaltaisen taulukon suoraan laskemalla todennäköisyyksiä.
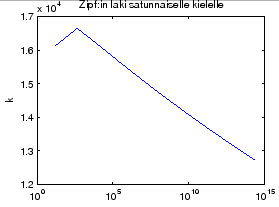
Koska samanpituiset sanat ovat yhtä todennäköisiä eikä niitä voi
asettaa yleisyysjärjestykseen, laskemme ![]() :n arvon vain yhdelle
samanpituisista sanoista. Tulokset on
esitetty taulukossa 1 ja piirretty kuvaan 1.
:n arvon vain yhdelle
samanpituisista sanoista. Tulokset on
esitetty taulukossa 1 ja piirretty kuvaan 1.
| 15 | 1111 | 16111 |
| 450 | 37.04 | 16648 |
| 13064 | 1.235 | 16129 |
| 378900 | 0.0412 | 15593 |
| 1098800 | 0.00137 | 15073 |
| 318660000 | 0.0000457 | 14570 |
Huomataan, että satunnaisellakin kielellä
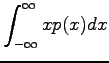 |
|||
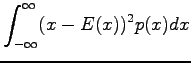 |
- a)
- Lasketaan odotusarvo yhden heiton silmäluvuksi. Noppa
laskeutuu jokaiselle 101:lle sivustaan yhtä todennäköisesti, eli
jokaisen tapahtuman todennäköisyys
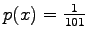 .
.
Odotusarvo:
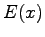

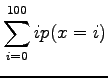

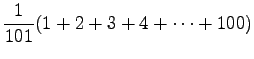

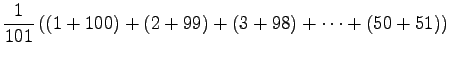

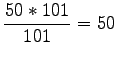
Varianssi voidaan laskea kaavalla:
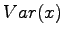

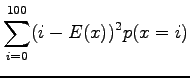

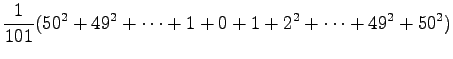

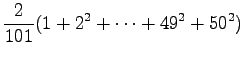
Nyt voimme käyttää avuksemme seuraava kaavaa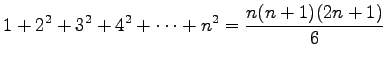
jolloin saamme tulokseksi
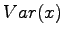

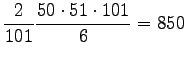
- b)
- Ratkaistaksemme tämän tehtävä, tarvitsemme muutamia
todennäköisyyslaskun peruskaavoja. Kaavat on tässä johdettu, mutta
niiden johtamisen osaaminen ei ole olennaista kurssin kannalta.
Riippumattomien satunnaismuuttujien summan oletusarvo
Olkoon satunnaismuuttujat x ja y riippumattomia. Lasketaan näiden satunnaismuuttujien summan oletusarvo.
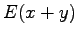

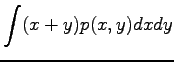

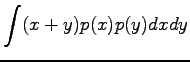

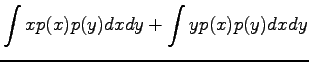

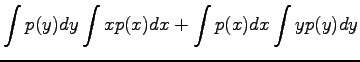

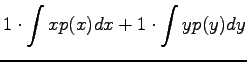

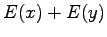
Vakiolla kerrotun satunnaismuuttujan varianssi
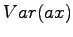

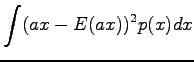

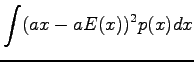

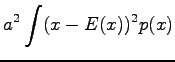

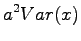
Riippumattomien satunnaismuuttujien summan varianssi
Olkoon satunnaismuuttujat x ja y riippumattomia. Lasketaan näiden satunnaismuuttujien summan varianssi.
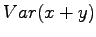

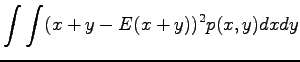

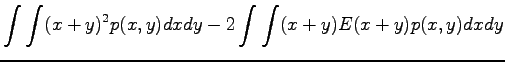
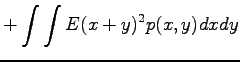

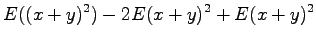

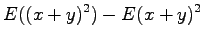

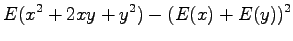

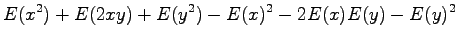

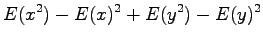
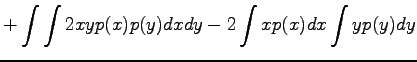

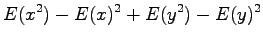

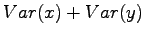
Tämän pakerruksen jälkeen päästään itse asiaan. Nyt halutaan laskea oletusarvo lauseelle
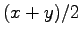 , missä
, missä 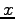 on ensimmäiseen heittoon
liittyvä satunnaismuuttuja ja
on ensimmäiseen heittoon
liittyvä satunnaismuuttuja ja 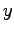 on toiseen heittoon liittyvä
satunnaismuuttuja.
on toiseen heittoon liittyvä
satunnaismuuttuja.
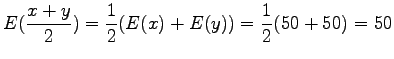
Huomaamme siis, että odotusarvo ei muutu. Entä miten käykään varianssin?
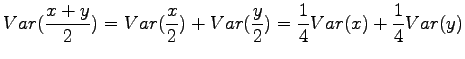
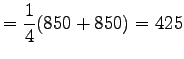
- c)
- Heitämme kymmentä noppaa, sovellamme edelle opittuja
tuloksia. Odotusarvo
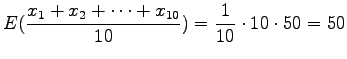
Varianssi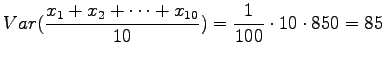
- d)
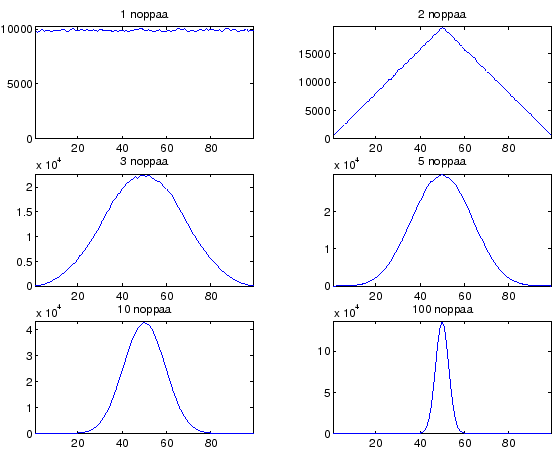
- Kun heitämme yhä useampaa noppaa, tarkentuu jakauma odotusarvon ympärille. Rajalla odotusarvo on 50 ja varianssi 0 eli saamme aina varmasti tulokseksi 50.
Odotusarvo ja varianssi eivät suinkaan kerro kaikkea jakaumasta. Kuvassa 2 on simuloitu matlabilla erilaisia määriä nopanheittoa. Huomaamme että jakauman muoto muuttuu, mitä useampaa nopaa heitetään. Muoto tulee lähemmäksi ja lähemmäksi normaalijakaumaa. Tämän takia useita luonnollisia ilmiöitä mallinnetaan normaalijakaumalla: Jos tulokseen vaikuttaa monta pientä satunnaista asiaa, tulos on normaalisti jakautunut. Tämä on myös hyvä tekosyy käyttää normaalijakaumaa, jolla saadaan laskut usein helppoon muotoon.
Formaalimpi todistelu siitä, että jakauma lähestyy normaalijakaumaa löytyy http:// mathworld.wolfram.com/CentralLimitTheorem.html
Merkitään lausekkeen minimoivaa parametrijoukkoa
Sijoitetaan tähän optimaaliset kuvauspituudet
Yhdistetään termit logaritmien laskusääntöä käyttäen:
Logaritmi on monotonisesti kasvava funktio, ja sen vastaluku siten monotonisesti laskeva, joten sama arvo saadaan maksimoimalla todennäköisyyksien tuloa:
Lopuksi muistetaan Bayesin kaavasta
Jakauma