Let's start from Bayes' theorem.
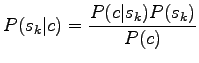 |
Now we are interested only in the order of probabilities, not the absolute values, so we can forget the normalization term
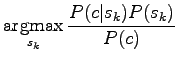 |
|||
In the equation the latter term is the prior for the word sense. It can be estimated for example by calculating how many of the words in the training corpus have appeared in the sense
Let's choose the nearest 10 words as the context:
The word we are studying would be in the middle,
Now we have:
Let's make the estimation easier by assuming that the words occur independently:
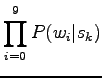 |
Finally, let's write the expression open:
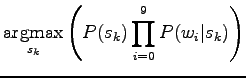 |
|||
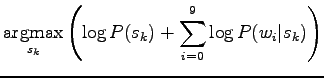 |
In the last row the formula is written in logarithmic form. This can be done, because taking the logarithm does not affect the order of the values.
None of the used approximations is totally correct, but the roughest error is probably the one of independency of the context words. However, this is the way of getting an easily feasible method.
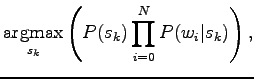 |
where
We need two estimates: probability
![]() that the word
that the word ![]() in the context occurs with the sense
in the context occurs with the sense ![]() , and prior probability
, and prior probability
![]() . As we have equal number of occurrences for the senses
sataa=rain and sataa=number, we can but set the
prior to
. As we have equal number of occurrences for the senses
sataa=rain and sataa=number, we can but set the
prior to ![]() .
.
Maximum likelihood (ML) estimation is applied in the course book.
In our problem we were asked to use priors, so let's define a small
prior that all words are of equal probability to the probability
![]() , and add it to the estimators with coefficient
, and add it to the estimators with coefficient
![]() .
This can be thought as if every known word had already occurred
0.5 times in both context types.
A large
.
This can be thought as if every known word had already occurred
0.5 times in both context types.
A large ![]() emphasises the meaning of the prior, and thus a small
evidence from the training set does not change it much.
emphasises the meaning of the prior, and thus a small
evidence from the training set does not change it much.
- a)
- Let's calculate the estimators needed in the first test sentence:
We see that for the first sense, all probability mass comes from the prior. For the comparison number (i.e. unnormalized probability) we get
The same calculations for the number sense:
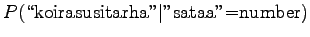
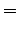
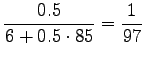
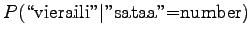
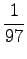

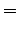
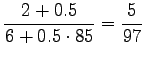
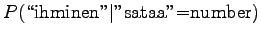
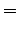
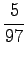
The comparison number is:
So according to the model, the number sense of ``sataa'' is more probable. - b)
- As we saw before, we can leave out all the words that have not occurred
in the contexts of either word, as they do not affect the order of
the comparison numbers. Let's use the tool that changes all
disambigous numbers to string ``num''. The needed probabilities are:
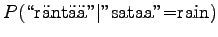
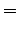
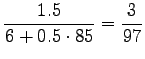

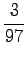
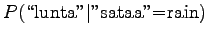
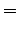
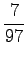
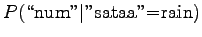
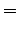
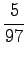
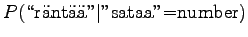
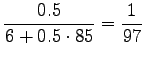

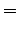
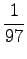
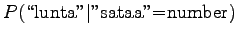
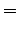
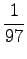

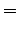
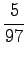
For the comparison numbers we get
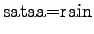
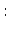
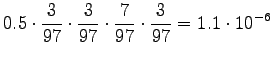
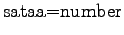
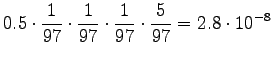
This time the word seems to mean raining. - c)
- For the third sentence,
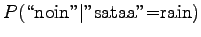
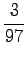
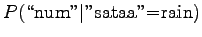
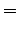
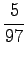

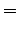
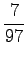

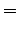
For the comparison numbers we get
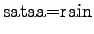
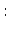
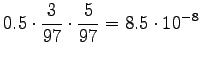
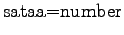
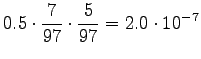
So it seems to be a number here. - d)
- For the last sentence the given training data does not change the probabilities for any direction. And because the priors were equal, the model cannot make any decision here.
Let's find the dictionary definitions for the words in the tested sentence. Those are compared to the dictionary definitions of two senses of the studied word. The meaning that has more mutual words with the words in the dictionary definitions of the other words (including the word itself) in the sentence is decided to be the correct one.
In this case, from the definition of ``ampuminen'', shooting, we find the words ``harjoitella'' and ``varusmies'' that are also in the test sentence. The word ``sarjatuli'' is found from the definition of ``kivääri'', so three points for shooting.
From the definition of ``ammuminen'', that is moo'ing, we find the word ``niityllä'', which is also in the test sentence. One point for moo'ing.
It seems that it is shooting for this one (![]() ).
).
Let's see how many hits the Google will give:
| prices | go up | 111000 |
| price | goes up | 88100 |
| 199100 | ||
| prices | slant | 58 |
| prices | lean | 2520 |
| prices | lurch | 21 |
| price | slants | 1 |
| price | leans | 63 |
| price | lurches | 114 |
| 2777 |
This example goes clearly for the sense ``go up''.
What about the next example? If we do the translation and search
using the given word order, we will get no hits (excluding the
hits for this exercise problem). So we try to find
documents where the words may occur in any order:
| want | shin | hoof | liver | or | snout | 260 |
| like | shin | hoof | liver | or | snout | 304 |
| covet | shin | hoof | liver | or | snout | 219 |
| desire | shin | hoof | liver | or | snout | 243 |
| 1026 | ||||||
| want | kick | poke | cost | or | suffer | 43500 |
We see that the verb meanings of the words win here, altough the nouns would probable be more correct. All searches are not even needed, because the first one already produces more hits than all of the other senses together. In addition, most of the hits returned by the first four searches were from dictionaries.
As the senses shin, hoof, liver and snout are much rarer than the verbs, they are found much less. In this situation we should probably normalize the search in some way. This example was harder than the first one also because this time the sentence was not a common and fixed phrase.
The problem is to estimate the probability of the sense ![]() when
we know the context
when
we know the context ![]() .
.
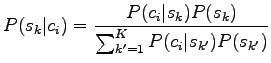 |
Let's use the Naive Bayes assumption presented in first problem, i.e. that the words
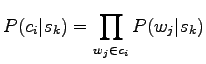 |
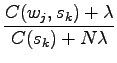
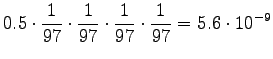
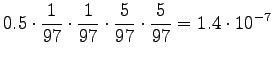
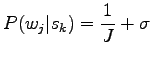
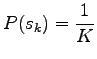
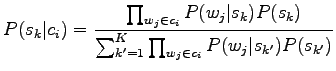
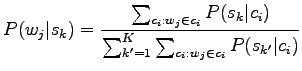
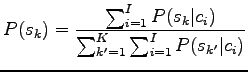
![\begin{figure}\centering\mbox{\subfigure[$P(w_j\vert s_0)$: Probability that the...
... the
sense $s_0$]{\epsfig{figure=sp.eps,width=0.45\linewidth}}}
\end{figure}](img80.png)