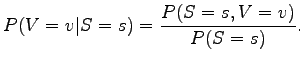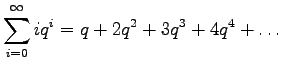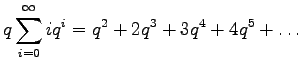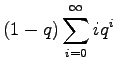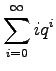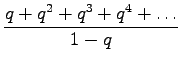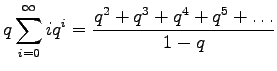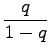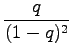- a)
- Let's use the definition of the entropy,
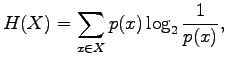
with given values:

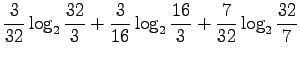
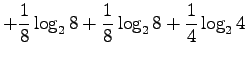

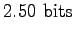
- b)
- For the solution we need the probability
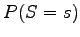 (a random substantive
is
(a random substantive
is 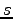 ). It can be obtained from the right margin probability of the
given table. In addition we need the probability
). It can be obtained from the right margin probability of the
given table. In addition we need the probability
The entropy of the source, as we know that the previous symbol was a substantive, is
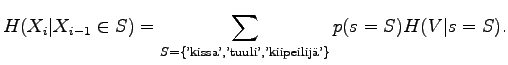
For this we need to calculate the conditional entropy
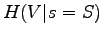 .
For the word 'kissa',
.
For the word 'kissa',
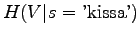



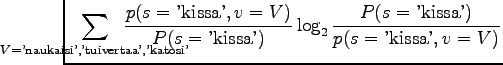

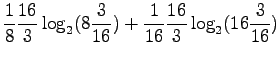

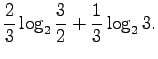
As we place the probabilities for each word in , we get
, we get
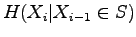

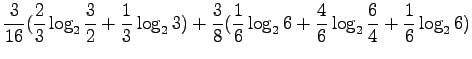
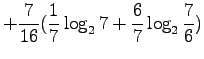

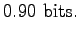
What is the probability for a random word to be ``kissa''? As both
categories ![]() and
and ![]() are of equal probability, the result is
are of equal probability, the result is
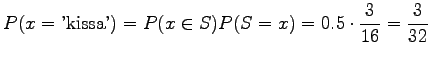 |
We note that the distribution in (a) is actually a marginal distribution for the joint distribution in (b).
To conclude, when we know the behavior of the source more accurately, the produced words are less suprising and we can code them with less bits (0.9 bit < 2.5 bit).
Let's denote the probabilities of the language as ![]() , and the
probabilities given by the model as
, and the
probabilities given by the model as ![]() . We want to calculate
the expected coding length of a sentence when it is coded with the
model:
. We want to calculate
the expected coding length of a sentence when it is coded with the
model:
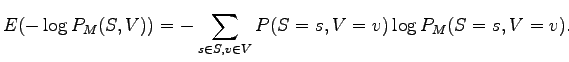 |
This measure is called cross-entropy.
For the model, the noun and the verb of a sentence are independent, so
![]() . By using that and writing the
sum open first for the nouns and then for the verbs we get:
. By using that and writing the
sum open first for the nouns and then for the verbs we get:
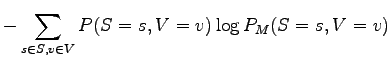 |
|||
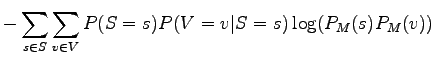 |
|||
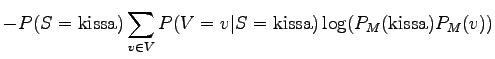 |
|||
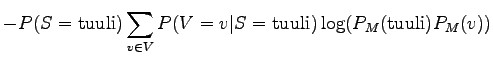 |
|||
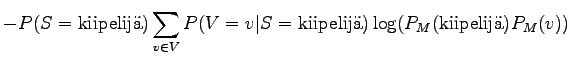 |
|||
![$\displaystyle - \frac{3}{16} \cdot
\big[\frac{1}{8}\frac{16}{3} \log(\frac{3}{32} \frac{1}{8}) +
\frac{1}{16}\frac{16}{3} \log(\frac{3}{32} \frac{1}{4}) \big]$](img34.png) |
|||
![$\displaystyle - \frac{3}{8} \cdot
\big[\frac{1}{16}\frac{8}{3} \log(\frac{3}{16...
...16} \frac{1}{8}) +
\frac{1}{16}\frac{8}{3} \log(\frac{3}{16} \frac{1}{4}) \big]$](img35.png) |
|||
![$\displaystyle - \frac{7}{16} \cdot
\big[\frac{1}{16}\frac{16}{7} \log(\frac{7}{32} \frac{1}{8}) +
\frac{3}{8}\frac{16}{7} \log(\frac{7}{32} \frac{1}{4}) \big]$](img36.png) |
|||
The average coding length (or cross-entropy) for a sentence is thus 5.01 bits.
Each sentence includes two words, so the average coding length for one word is 2.50 bits. The result equals to what was calculated in part (a). This is due to the fact that the distribution over which the expected value of the coding lengths is calculated is the same.
- a)
- Each of the 30 elementary events has a probability of
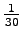 .
Just place these into the definition of entropy:
.
Just place these into the definition of entropy:
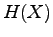

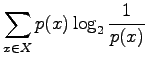

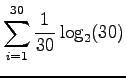

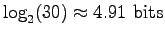
- b)
- To generate a one letter word, the given random language should
generate two symbols, i.e. word boundary after something else.
The probability for this is
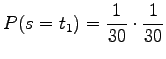
and there are 29 words of this kind.Respectively, the probability of a word of two letters is
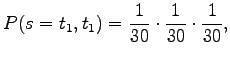
there are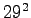 words of this kind, and so on.
words of this kind, and so on.
Let's calculate the entropy:



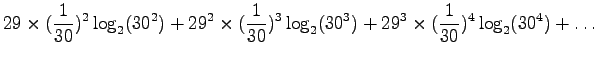


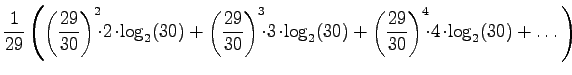


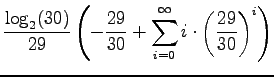
Multiply both sides by
Subtract equation 2 from equation 1.
Multiply equation 4 by
Subtract equation 4 from equation 5 to obtain the solution:
(In order to make the subtractions and the multiplications,
Applying this to the orginal problem, we obtain the result of
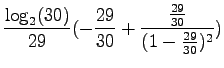 |
|||
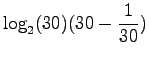 |
|||
At first glance this may seem confusing: Shouldn't the result be same as in part (a)? A quick verification shows that it is indeed right: Expectation value for word length is 29, so entropy per symbol is approximately
There is also another reason for the results not to be exactly same: The first source may generate successively two word boundaries, the second source can not. In consequence, the second source has a bit lower entropy.
- a)
- Let's mark the perplexities for the models as
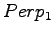 ,
, 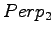 and
and 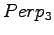 .
.
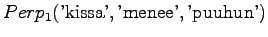
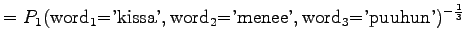
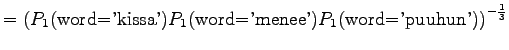
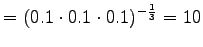
The model always chooses one of ten different words with equal probabilities, so this is exactly what we should get.
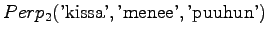

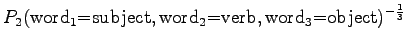

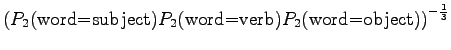

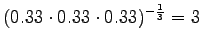
The model selects always one out of three options, so also this result seems reasonable.
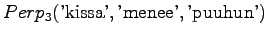

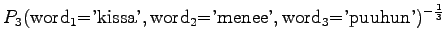

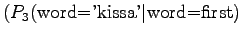



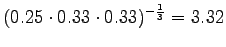
The last model chooses from 3.32 words on average.The models 1 and 3 are comparable, as they operate with the same set of symbols. Of these two, model 3 seems to be much better.
Model 2 is not comparable to others, as it operates on a smaller set of symbols and gets a low entropy because of that. An extreme example would be a model for which every word goes to the same category. This kind of model would never be ``surprised'', and the perplexity would be one.
- b)
- Let's examine the next test sentence. For the first model,
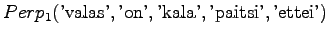

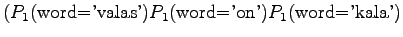
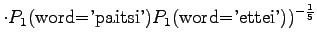

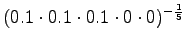

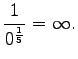
We note that perplexity cannot be calculated, if the model gives a probability of zero for any word in the test set. Often those words are excluded. This way the result is
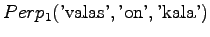

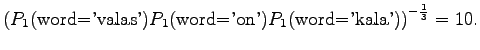
To report a meaningful result, the perplexity is not enough, but we should also count the words that were not recognized by the model. In this case,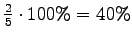 words were out of model's
vocabulary. For the next model,
words were out of model's
vocabulary. For the next model,
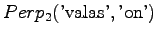

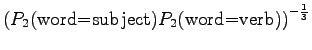

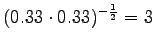
This model misses 60% of the words.Also model 3 recognizes only the two first words.
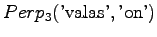




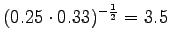
The out-of-vocabulary (OOV) rate is 60%.As before, model 2 is not comparable with the rest. Models 1 and 3 can be compared, as long as we take into account the out-of-vocabulary rates. Model 1 covers more vocabulary, but model 3 gives better perplexity. Creating a language model is often balancing between these properties.