In the following table there are the definitions of the five first
measures and the results for applying them.
|
F-measure is defined using both the precision and recall:
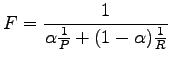 |
where
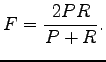 |
For the first engine
When calculating uninterpolated average precision, we go through the list of returned documents, and whenever a relevant document is seen, we calculate the precision over the documents processed so far. Relevants that were not returned are taken into account with a zero precision. Then we take an average over the precisions.
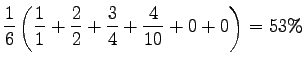 |
|||
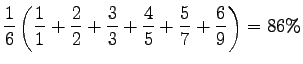 |
The idea in Residual Inverse Document Frequency (RIDF) is that we can model the occurrences of a word using a Poisson distribution. This works well for words that are evenly distributed in a corpus. Contentually important words usually occur in groups inside the documents that discuss the corresponding matter, and therefore Poisson distribution gives an incorrect estimation for their frequencies. In RIDF we measure the difference between IDF and Poisson distributions. The more difference we have, the more does the word tell about the document. (Note: There are many errors in this section of the course book's first edition.)
Actual calculations are the following: On average, word ![]() occurs
occurs
![]() times in a document. The probability
for that in a certain document word
times in a document. The probability
for that in a certain document word ![]() occur
occur ![]() times is
obtained from the Poisson distribution:
times is
obtained from the Poisson distribution:
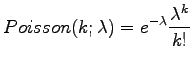 |
RIDF is defined as
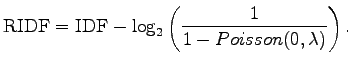 |
I.e., we take from the Poisson distribution the probability that the word occurs at least once in the document (
Simplifying the expression of RIDF:
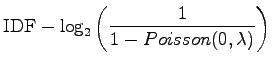 |
|||
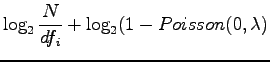 |
|||
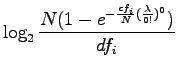 |
|||
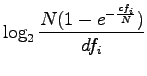 |
Assigning the values:
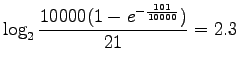 |
|||
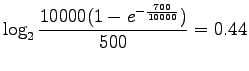 |
We see that RIDF weighted the word ![]() 2.5 times more than IDF.
Thus both methods estimate that
2.5 times more than IDF.
Thus both methods estimate that ![]() is a more relevant search term
than
is a more relevant search term
than ![]() .
.
In Singular Value Decomposition (SVD) we decompose the matrix
Here
|
|
|
|
|
We reduce the inner dimension to two by taking only the two largest
eigenvalues from ![]() and leaving the rest of the dimensions out from
the matrices
and leaving the rest of the dimensions out from
the matrices ![]() and
and ![]() . Now the similarity of the documents can be
compared using the matrix
. Now the similarity of the documents can be
compared using the matrix ![]() . If
. If ![]() 's columns are scaled to
unity, it is easy to calculate correlations between rows. This kind of
a scaled matrix is in table 7. (Similarity of words
could be compared from
's columns are scaled to
unity, it is easy to calculate correlations between rows. This kind of
a scaled matrix is in table 7. (Similarity of words
could be compared from ![]() .) From the correlation matrix (table
8) we see that the Formula 1 and astronomy related
articles correlate much more inwardly than crosswise. Documents
.) From the correlation matrix (table
8) we see that the Formula 1 and astronomy related
articles correlate much more inwardly than crosswise. Documents ![]() and
and ![]() that were totally uncorrelated before, are now clearly
correlated. We have projected the data to two-dimensional space, and
similar articles have ended up near each other in that reduced
dimension.
that were totally uncorrelated before, are now clearly
correlated. We have projected the data to two-dimensional space, and
similar articles have ended up near each other in that reduced
dimension.