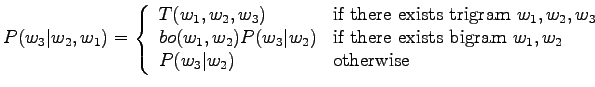a) The task is to estimate the probability of the word following words ``tuntumaan jo'' (feel already). The possible followers are words
- ja [and]
- hyvältä [good]
- kumisaapas [rubber boot]
- keväältä [(like) spring (season)]
- ilman [without]
- päihtyneeltä [drunk]
- turhalta [vain]
- koirineen [with (his) dogs]
- öljyiseltä [oily]
- Turku [a city in Finland]
Give a probability value for each so that they sum up to one. Compare the estimates given by yourself to ones calculated directly from a text corpus.
b) Now you know the full beginning of the sentence, which is ``Leuto sää ja soidinmenonsa aloittaneet tiaiset ovat saaneet helmikuun tuntumaan jo'' (free translation: ``Mild weather and the titmice that have started their displays have made the February feel already''). Estimate the same probabilities using this full context.
c) What kind of knowledge would a language model need to order to match up with a human in the b) case?
(Word used in the original sentence is found on the next page.)
- a)
- ...maximum likelihood estimates
- b)
- ...ML estimates with Laplace smoothing
- c)
- ...ML estimates with Lidstone (additive) smoothing
with parameter
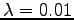 .
.
Use an interpolated bigram model to calculate probabilities
for the examples of the previous exercise. Smooth the bigram
estimates using absolute discounting with discount parameter
![]() .
.