![$\displaystyle A=\left[ \begin{array}{ccc} 0.8 & 0.15 & 0.05 \\ 0.4 & 0.5 & 0.1 \\ 0.3 & 0.3 & 0.4 \\ \end{array} \right]$](img4.png) |
Element
- a)
- Draw Markov chain for the weather.
- b)
- Today it is cloudy. What is the probability of the following sequence of five days: Tomorrow it rains, day after tomorrow is cloudy, and after it we have three sunny days.
- c)
- On average, how many successive sunny days there are?
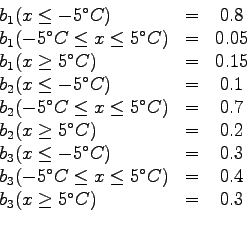
- a)
- After three days the holiday ends and it is time to fly back.
You want to estimate what kind of weather it is when you come
back, in order to dress appropriately. The temperatures in the home
town were
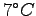 ,
, 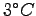 and
and
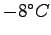 . Calculate
the probabilities of the three weather types on the day of returning.
It is recommended to use the forward algorithm, brute force will be
very time consuming.
. Calculate
the probabilities of the three weather types on the day of returning.
It is recommended to use the forward algorithm, brute force will be
very time consuming.
- b)
- In the airplane you speculate what kind of weather it has been in
home during the holidays. Find the most probable state sequence.
Viterbi algorithm uses the least number of calculations.