| W | P(W) | |
| 'kissa' | (cat) |
|
| 'tuuli' | (wind) |
|
| 'kiipeilijä' | (climber) |
|
| 'naukaisi' | (meowed) |
|
| 'tuivertaa' | (blows) |
|
| 'katosi' | (disappeared) |
|
- a)
- Assume that a source generates values for a random variable
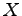 according to the table above. What is the entropy of the source
according to the table above. What is the entropy of the source 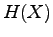 ?
?
- b)
- According to further examination, the language has a sentence
structure 'SV' with categories S
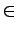 {'kissa', 'tuuli', 'kiipeilijä'}
and V
{'kissa', 'tuuli', 'kiipeilijä'}
and V 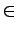 {'naukaisi', 'tuivertaa', 'katosi'}. The joint distribution
P(S,V) of the variables is the following:
{'naukaisi', 'tuivertaa', 'katosi'}. The joint distribution
P(S,V) of the variables is the following:
'naukaisi' 'tuivertaa' 'katosi' 'kissa' 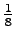
0 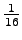
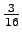
'tuuli' 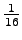
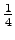
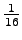
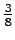
'kiipeilijä' 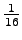
0 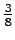
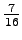
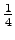
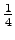
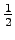
What is the entropy of the source when we know that the previous symbol belongs to the set S, i.e. what is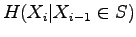 ?
?
- c)
- Assume that a language is generated by the model of part b.
Now we model the two-word sentences of the language with the model
given in part a. Calculate the average number of bits needed to encode
the sentences with optimal code lengths given by the model.
- a)
- The source generates symbols one by one. What is the entropy of the source?
- b)
- The source generates one word (one or more non-boundary symbols followed by a word boundary) at a time. Each word is treated as a whole. What is the entropy of the source?
| Model 1 | Model 2 |
| P(sana='kissa')=0.1 | P(word=subject)=0.33 |
| P(sana='koira')=0.1 | P(word=verb)=0.33 |
| P(sana='valas')=0.1 | P(word=object)=0.33 |
| P(sana='kala')=0.1 | |
| P(sana='istui')=0.1 | |
| P(sana='menee')=0.1 | |
| P(sana='on')=0.1 | |
| P(sana='puuhun')=0.1 | |
| P(sana='kuuhun')=0.1 | |
| P(sana='suuhun')=0.1 |
| Model 3 | |
| P(sana='kissa' | word=first) | =0.25 |
| P(sana='koira' | word=first) | =0.25 |
| P(sana='valas' | word=first) | =0.25 |
| P(sana='kala' | word=first) | =0.25 |
| P(sana='istui' | previous_word |
=0.33 |
| P(sana='menee' | previous_word |
=0.33 |
| P(sana='on' | previous_word |
=0.33 |
| P(sana='puuhun' | previous_word |
=0.33 |
| P(sana='kuuhun' | previous_word |
=0.33 |
| P(sana='suuhun' | previous_word |
=0.33 |
As a test set for the models, we have two sentences:
- a)
- Kissa menee puuhun. (Cat goes to tree.)
- b)
- Valas on kala paitsi ettei. (Whale is fish except not.)
Perplexity can be defined as the inverse of the geometric mean of the probabilities: