Let us observe a stemming program for Finnish. By using the context, it can conduct whether the stem for word-form ``siitä'' is ``se'' (it) or ``siittää'' (conceive). For a word-form of ``se'' the program can determine the right stem for probability of 0.95. The same holds for the word-forms of ``siittää''. Because the stem ``se'' is much more common, only one of a thousand ``siitä'' should be conducted to the stem ``siittää''.
The program tells that for an occurred word-form ``siitä'', the corresponding stem is ``siittää''. What is the probability that the program is correct?
So called Zipf's law is often referred when simple statistics are
calculated from a language. Let the words be tabulated so that the
most common word comes first (![]() ), and the rest follow by the order
of frequency (
), and the rest follow by the order
of frequency (
![]() ). Next to the word is written how many
times it occurred it the text (
). Next to the word is written how many
times it occurred it the text (![]() ). Zipf alleges that
). Zipf alleges that
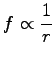 |
i.e.
Does this apply to a randomly generated language, that has 30 letters including the word boundary?
- a)
- A 101-sided dice is thrown. The sides have numbers 0 - 100.
Calculate expectation value and variance for the result. Sketch a
graph for probability p(X) when X is the result.
- b)
- Two similar 101-sided dices are thrown, and the sum of results
is divided by two.
Calculate expectation value and variance. Sketch a graph for probability
p(X) when X is the sum divided by 2.
- c)
- Now ten dices are thrown. Again, draw a graph for the sum of
results divided by the number of dices.
- d)
- Let's use all the dices of the world (
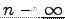 ).
What kind of distribution do we have? Draw a graph.
).
What kind of distribution do we have? Draw a graph.
Ideal MDL is of little practical use, since it has been shown that it is impossible to design an algorithm that finds the shortest possible Turing machine. Therefore there exists several variations, of which one quite common is so called two-part coding scheme.
In two-part coding scheme we first select a model class that can
describe some data given the model parameters ![]() . The goal is to
describe and send a set of data,
. The goal is to
describe and send a set of data, ![]() , that is assumed to be generated
by a model of the decided class, with the minimum number of bits
possible. As the receiver does not know the parameters that we choose,
also they must be sent. Denote
, that is assumed to be generated
by a model of the decided class, with the minimum number of bits
possible. As the receiver does not know the parameters that we choose,
also they must be sent. Denote ![]() as the description length
needed to encode the parameters, and
as the description length
needed to encode the parameters, and
![]() as the
description length needed to encode the data when the parameters are
known. Thus we need to minimize the total code length
as the
description length needed to encode the data when the parameters are
known. Thus we need to minimize the total code length
![]() .
.
In statistical modeling, the coding of the model class corresponds to
probability distribution
![]() , and the coding of parameters
to distribution
, and the coding of parameters
to distribution ![]() . From information theory we know that if
probability of a message is
. From information theory we know that if
probability of a message is ![]() , the minimum code length for the
message is
, the minimum code length for the
message is
![]() bits. Show that the optimal selection of the
parameters in two-part coding scheme equals to Maximum A Posteriori
estimation.
bits. Show that the optimal selection of the
parameters in two-part coding scheme equals to Maximum A Posteriori
estimation.