First of the given probabilities,
![]() ,
tells that is we see a word of three letters, the probability that it is
an abbreviation is 0.8, and 0.2 for something else.
Next one,
,
tells that is we see a word of three letters, the probability that it is
an abbreviation is 0.8, and 0.2 for something else.
Next one,
![]() ,
tells that the probability for a random word being exactly three
letters long is
,
tells that the probability for a random word being exactly three
letters long is ![]() .
.
The probability for a random word being three letter abbreviation
is get by product of the given probabilities. First we look how
probable it is for a word to be three letters long, then how
probable it is to be abbreviation when being three letters:
To answer the given question, we need the Bayes' theorem:
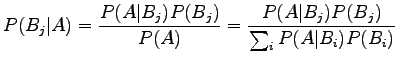 |
Using the theorem, the probability that the program is right, when it tells that the stem is ``siittää'', is:
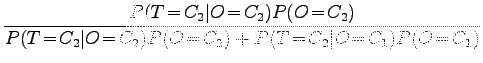 |
|||
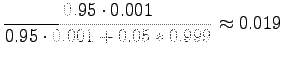 |
To generate a one letter word, the given random language should generate two symbols, i.e. word boundary after something else. The probability for this is
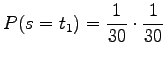 |
and there are 29 words of this kind.
Respectively, the probability of a word of two letters is
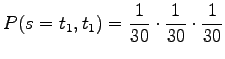 |
There are
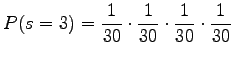 |
and the number of words is
As the probability of the word is directly proportional to its
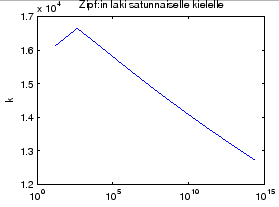
expected incidence in the test data, we can make a table similar
to the table 1.3 in the book by directly calculating probabilities.
As words of same length have equal probability, and they cannot be
sorted by frequency, we count the ![]() value for only one word per
length. The results are presented in table 1 and drawn
to Figure 1.
value for only one word per
length. The results are presented in table 1 and drawn
to Figure 1.
| 15 | 1111 | 16111 |
| 450 | 37.04 | 16648 |
| 13064 | 1.235 | 16129 |
| 378900 | 0.0412 | 15593 |
| 1098800 | 0.00137 | 15073 |
| 318660000 | 0.0000457 | 14570 |
We can see that the even for a random language,
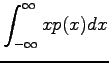 |
|||
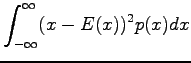 |
- a)
- Let's calculate the expected value for one toss of the dice.
Each side of the dice is of equal probability, so the
probability of each event is
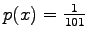 .
.
Expectation value:
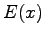

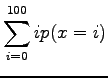

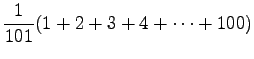

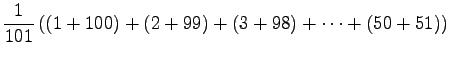

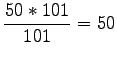
Variance:
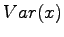

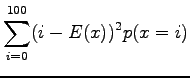

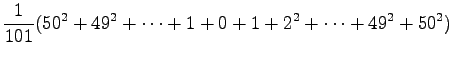

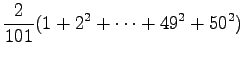
Now we can use formula
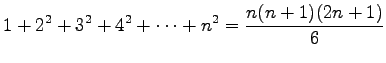
to get the result:
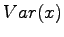

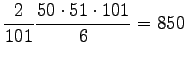
- b)
- To solve the problem, we will need a couple of basic formulas for
probability calculation, which are derived here. (However, the
derivations are not essential for the course.)
Expectation value of the sum of independent random variables
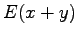

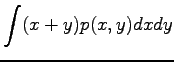

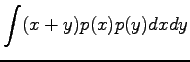

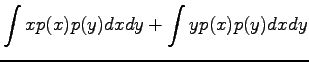

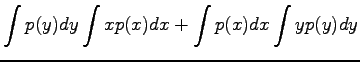

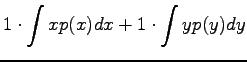

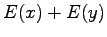
Variance of a random variable multiplied by a constant
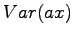

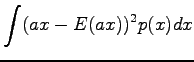

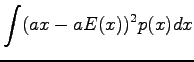

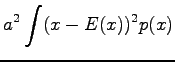

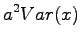
Variance of the sum of independent random variables
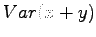

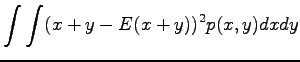

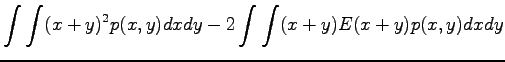
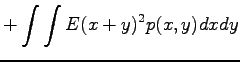

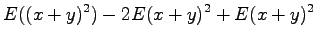

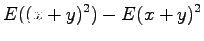

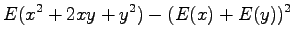

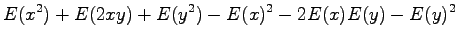

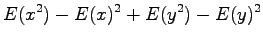
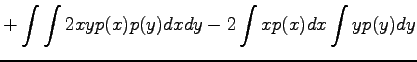

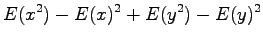

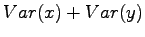
Now we have all the needed formulas. We want to calculate expectation value for the sum
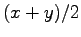 , where
, where 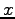 is the random variable corresponding
to the first throw and
is the random variable corresponding
to the first throw and 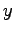 to the second.
to the second.
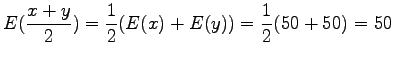
We notice that the expectation value does not change. What about variance, then?
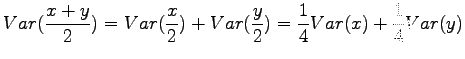
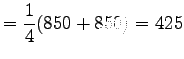
- c)
- We throw ten dices. Using the learned solutions:
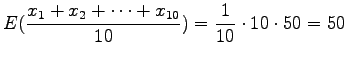
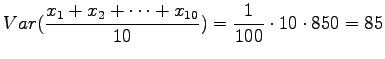
- d)
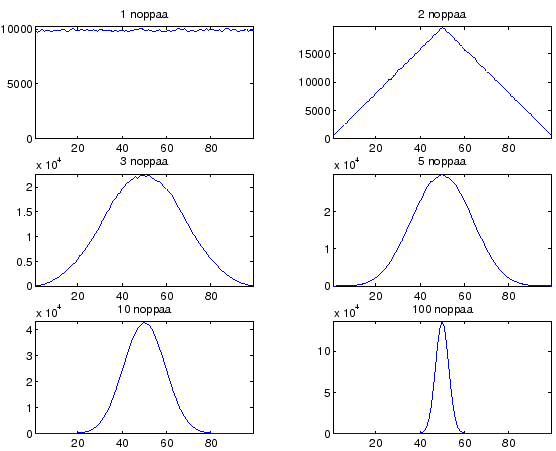
- As we throw even more dices, the distribution will sharpen around the expectation value. At the inifinite, expectation value is 50 and variance 0, which means that we will always get a result of 50.
The expectation value and variance do not tell everything about the distribution. In figure 2 there are results for varying number of dice tosses simulated using Matlab. The shape of the distribution moves nearer to the normal (gaussian) distribution as the number of dices grow. This is why natural phenomena are often modelled using normal distribution: If many small random events affect to the result, it will be normal distributed. This is also is good excuse for transforming calculations to easier forms.
More formal proof for that the distribution will approach normal is found from http:// mathworld.wolfram.com/CentralLimitTheorem.html
The goal is to minimize the total code length
Let's denote the set of parameters that minimize the previous expression as
Now we substitute the code lengths for their optimal values
The logarithmic terms can be combined using the product rule of logarithms:
As logarithm is a monotonically increasing function, and thus its complement monotonically decreasing, the minimum can be obtained by maximixing the product of the two probabilities:
Finally, from Bayes' theorem we get
Probability