T-61.271 Information visualization
Exercise 7. Thu 4.12.2003:12-14 T4
- Focus and context
- Visualizing text
- 1.
- Fisheye view.
a. Assume that a data structure (e.g. contents of a book) that can
be represented by a tree of height 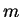 and brancing factor
and brancing factor 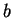 . How
many steps does it take to traverse from one leaf node to another
by traversing though fisheye-views of the tree?
. How
many steps does it take to traverse from one leaf node to another
by traversing though fisheye-views of the tree?
b. Present a (short) program code of you choice by setting the
focus on some line and using the fisheye view.
- 2.
- The size of vocabulary can be reduced by removing some rare and
very common words ("and", "the", ...). What could you do to reduce
the vocabulary further?
- 3.
- How are the distances and the resulting document presentations
in 2D space affected if the document vectors are not normalized
(not normalized means that
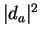 is generally not equal to
is generally not equal to
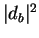 ,
, 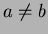 )?
)?
- 4.
- Random projection can be used to reduce the dimension of the
document vectors:
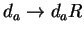 , Under what condition
does the expectation of the similarity between two
document vectors (
, Under what condition
does the expectation of the similarity between two
document vectors (
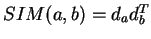 ) remain unchanged (i.e. how
should you generate entries for the matrix
) remain unchanged (i.e. how
should you generate entries for the matrix 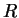 )? How do you expect
the variance of the similarity
)? How do you expect
the variance of the similarity 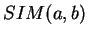 behave as a
function of the final dimensionality
behave as a
function of the final dimensionality 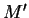 of the document vector?
of the document vector?
[Hints:
http://www.hut.fi/Yksikot/Kirjasto/Diss/2000/isbn9512252600/,
article 4,
http://www.cis.hut.fi/sami/abstracts.html#ijcnn98]
- 5.
- Dimension reduction methods, such as the use of feature words,
random projection or latent semantic indexing can be useful if you
use PCA or SOM to present the documents in 2D space. However, these
dimension reduction methods are useless if you use MDS. Why? Would
you expect to be able to represent the one million documents of
WEBSOM by using MDS instead of SOM?
Jarkko Venna
2003-11-28
![]() and brancing factor
and brancing factor ![]() . How
many steps does it take to traverse from one leaf node to another
by traversing though fisheye-views of the tree?
. How
many steps does it take to traverse from one leaf node to another
by traversing though fisheye-views of the tree?