- Devise a method based on principal component analysis performing these steps.
- Is the proposed method unique?
- Show how a single
column, that is of height
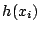 in the interval
in the interval
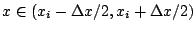 and zero elsewhere, can be constructed with a two-layer
MLP. Use two hidden units and the sign function as the activation
function. The activation function of the output unit is taken to be
linear.
and zero elsewhere, can be constructed with a two-layer
MLP. Use two hidden units and the sign function as the activation
function. The activation function of the output unit is taken to be
linear.
- Design a two-layer MLP consisting of such simple
sub-networks which approximates function
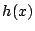 with a precision
determined by the width and the number of the columns.
with a precision
determined by the width and the number of the columns.
- How does the approximation change if tanh is used instead of sign as an activation function in the hidden layer?
![$\displaystyle E\left( \sum_{i=1}^C [y_i(\mathbf{x})-t_i]^2 \right),$](img9.gif) |
where
- Show
that the theoretical solution of the minimization problem is
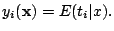
- Show that if
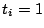 when
when
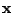 belongs to class
belongs to class 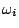 and
and
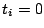 otherwise, the theoretical solution can be written
otherwise, the theoretical solution can be written
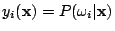
which is the optimal solution in a Bayesian sense. - Sometimes the number of the output neurons is chosen to be less than the
number of classes. The classes can be then coded with a binary code. For
example in the case of 8 classes and 3 output neurons, the desired
output for class
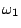 is
is ![$ [0,0,0]^T$](img19.gif) , for class
, for class
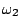 it is
it is ![$ [0,0,1]$](img21.gif) and so on. What is the theoretical solution
in such a case?
and so on. What is the theoretical solution
in such a case?
![\begin{figure}%%[h]
\centering\epsfig{file=function_approximation.eps,width=130mm}\end{figure}](img22.gif)