where
-
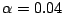
-
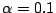
-
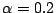
- What is the condition for the convergence of this method?
![$\displaystyle {\cal E} (\mathbf{w})= \frac{1}{2} \left[ \delta \Vert \mathbf{w} - \mathbf{w}(n) \Vert^2 + \sum_{i=1}^n e_i^2(\mathbf{w}) \right]$](img10.gif) |
yields the the following update rule for the weights:
All quantities are evaluated at iteration step
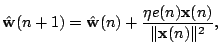 |
where
where
- Assuming that the input vector
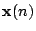 and desired response
and desired response 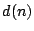 are drawn from a stationary environment,
show that
are drawn from a stationary environment,
show that
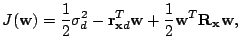
where![$ \sigma_d^2=E[d^2(n)]$](img23.gif) ,
,
![$ \mathbf{r}_{\mathbf{x}d}=E[\mathbf{x}(n)d(n) ]$](img24.gif) , and
, and
![$ \mathbf{R}_{\mathbf{x}}=E[\mathbf{x}(n)\mathbf{x}^T(n) ]$](img25.gif) .
.
- For this cost function, show that the gradient vector and
Hessian matrix of
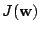 are as follows, respectively:
are as follows, respectively:
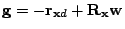 and
and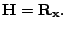
- In the LMS/Newton algorithm, the gradient vector
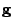 is
replaced by its instantaneous value. Show that this algorithm,
incorporating a learning rate parameter
is
replaced by its instantaneous value. Show that this algorithm,
incorporating a learning rate parameter 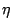 , is described by
, is described by
![$\displaystyle \Hat{\mathbf{w}}(n+1)=\Hat{\mathbf{w}}(n)+\eta \mathbf{R}_{\mathbf{x}}^{-1}\mathbf{x}(n)\left[d(n)-\mathbf{x}^T(n)\Hat{\mathbf{w}}(n)\right].$](img30.gif)
The inverse of the correlation matrix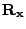 ,
assumed to be positive definite, is calculated ahead of time. (Haykin 3.8)
,
assumed to be positive definite, is calculated ahead of time. (Haykin 3.8)
- Construct a linear classifier which is able to
separate the following two-dimensional samples correctly:
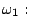
![$\displaystyle \{[2,1]^T\},$](img36.gif)
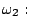
![$\displaystyle \{[0,1]^T, [-1,1]^T \}.$](img38.gif)
- Is it possible to construct a linear classifier which is able to
separate the following samples correctly?
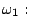
![$\displaystyle \{ [2,1]^T, [3,2]^T \},$](img39.gif)
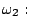
![$\displaystyle \{ [3,1]^T,[2,2]^T \}$](img40.gif)
Justify your answer.