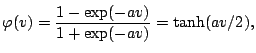 |
where
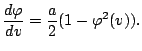 |
What is the value of this derivate at the origin? Suppose that the slope parameter
- Show that the McCulloch-Pitts formal model of a neuron may be approximated by a sigmoidal neuron (i.e., neuron using a sigmoid activation function with large synaptic weights).
- Show that a linear neuron may be approximated by a sigmoidal neuron with small synaptic weights.
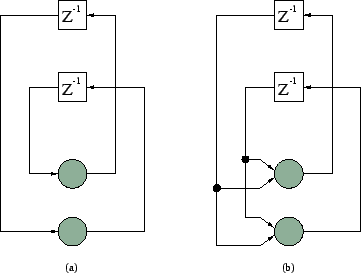
- Figure 1(a) shows the
signal-flow graph of a recurrent network made up of two neurons. Write
the nonlinear difference equation that defines the evolution of
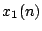 or that of
or that of 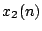 . These two variables define the outputs of the top
and bottom neurons, respectively. What is the order of this equation?
. These two variables define the outputs of the top
and bottom neurons, respectively. What is the order of this equation?
- Figure 1(b) shows the signal-flow graph of a recurrent network consisting of two neurons with self-feedback. Write the coupled system of two first-order nonlinear difference equations that describe the operation of the system.