Tik-61.261 Principles of Neural Computing
Raivio, Venna
Exercise 12
- It is sometimes said that the SOM algorithm preserves the
topological relationships that exist in the input space. Strictly
speaking, this property can be guaranteed only for an input space of
equal or lower dimensionality than that of the neural lattice. Discuss
the validity of this statement. (Haykin, Problem 9.3)
- It is said that the SOM algorithm based on competitive learning
lacks any tolerance against hardware failure, yet the algorithm is
error tolerant in that a small perturbation applied to the input
vector causes the output to jump from the winning neuron to a
neighboring one. Discuss the implications of these two
statements. (Haykin, Problem 9.4)
- In this problem we consider the optimized form of the learning
vector quantization algorithm (see Section 9.7, Haykin) developed by
Kohonen. We wish to arrange for the effects of the corrections to the
Voronoi vectors, made at different times, to have equal influence when
referring to the end of the learning period.
- First, show that Equation (9.30)
and Equation (9.31)
may be integrated into a single equation, as follows:
In the above equations,
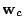 is the Voronoi
vector closest to the input vector
is the Voronoi
vector closest to the input vector
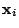 ,
,
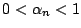 is a
learning constant, and
is a
learning constant, and 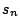 is a sign function depending on the
classification result of the
is a sign function depending on the
classification result of the 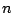 th input vector
th input vector
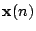 :
:
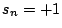 if classification is correct, otherwise
if classification is correct, otherwise 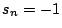 .
.
- Hence, show that the optimization criterion described at the
beginning of the problem is satisfied if
which yields the optimized value of the learning constant
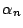 as
as
(Haykin, Problem 9.6)
- The following algorithm introduced by J. Friedman can be used for
speeding up winner search in the SOM algorithm: 1) Evaluate
the Euclidean distance between the input vector and weight vector
whose projections on some coordinate axis are least apart, 2) Examine
the weight vectors in the increasing order of their projected distances
to the input vector. Continue this until a weight vector whose
projected distance to the input vector is greater than the smallest Euclidean distance
calculated so far is found. At this point of the algorithm, the winning neuron
has been found.
Apply the algorithm described above for the problem illustrated in
Figure 1.
- Find the winning neuron when the weight vectors and the input
vector are projected onto
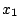 -axis. Show that the weight
vector found by the algorithm is indeed the winning one. How many
Euclidean distances one must evaluate for finding it?
-axis. Show that the weight
vector found by the algorithm is indeed the winning one. How many
Euclidean distances one must evaluate for finding it?
- Repeat the search but project the vectors onto
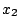 -axis
this time.
-axis
this time.
- Which one of the two searches was the fastest? Are there some general
rules on how the projection axis should be chosen?
Figure 1:
The weight vectors (o) among which the nearest one to the
input vector (x) has to be found.
![\begin{figure}%%[h]
\centering\epsfig{file=finding_nearest_neighbors.eps,width=130mm}\end{figure}](img17.gif) |
Jarkko Venna
2005-04-19
![$\displaystyle \mathbf{w}_c(n+1)=\mathbf{w}_c(n)+\alpha_n[\mathbf{x}_i-\mathbf{w}_c(n)]$](img1.gif)
![$\displaystyle \mathbf{w}_c(n+1)=\mathbf{w}_c(n)-\alpha_n[\mathbf{x}_i-\mathbf{w}_c(n)]$](img2.gif)
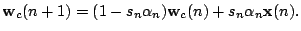
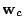 is the Voronoi
vector closest to the input vector
is the Voronoi
vector closest to the input vector
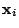 ,
,
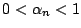 is a
learning constant, and
is a
learning constant, and 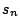 is a sign function depending on the
classification result of the
is a sign function depending on the
classification result of the 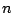 th input vector
th input vector
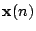 :
:
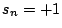 if classification is correct, otherwise
if classification is correct, otherwise 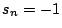 .
.
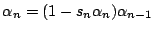
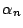 as
as
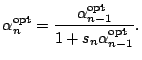
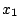 -axis. Show that the weight
vector found by the algorithm is indeed the winning one. How many
Euclidean distances one must evaluate for finding it?
-axis. Show that the weight
vector found by the algorithm is indeed the winning one. How many
Euclidean distances one must evaluate for finding it?
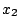 -axis
this time.
-axis
this time.
![\begin{figure}%%[h]
\centering\epsfig{file=finding_nearest_neighbors.eps,width=130mm}\end{figure}](img17.gif)