Tik-61.261 Principles of Neural Computing
Raivio, Venna
Exercise 11
- The weights of the neurons of a Self-organizing map (SOM) are
updated according to the following learning rule:
where 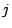 is the index of the neuron to be updated,
is the index of the neuron to be updated, 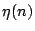 is the
learning-rate parameter,
is the
learning-rate parameter,
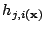 is the neighborhood
function, and
is the neighborhood
function, and
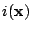 is the index of the winning neuron for
the given input vector
is the index of the winning neuron for
the given input vector
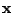 . Consider an example where
scalar values are inputted to a SOM consisting of three neurons. The
initial values of the weights are
. Consider an example where
scalar values are inputted to a SOM consisting of three neurons. The
initial values of the weights are
and the inputs are randomly selected from the set:
The Kronecker delta function is used as a neighborhood function. The
learning-rate parameter has a constant value 0.02. Calculate a few
iteration steps with the SOM learning algorithm. Do the weights converge?
Assume that some of the initial weight values are so far from the
input values that they are never updated. How such a situation could
be avoided?
- Consider a situation in which scalar inputs of a
one-dimensional SOM are distibuted according to the probability
distribution function
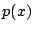 . A stationary state
of the SOM is reached when the expected changes in the weight
values become zero:
. A stationary state
of the SOM is reached when the expected changes in the weight
values become zero:
What are the stationary weight values in the following cases:
-
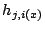 is a constant for all
is a constant for all 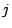 and
and 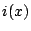 , and
, and
-
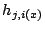 is the Kronecker delta function?
is the Kronecker delta function?
- Assume that the input and weight vectors of a SOM consisting of
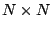 units are
units are 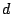 -dimensional and they are compared by using Euclidean
metric. How many multiplication and adding operations are required for finding the
winning neuron. Calculate also how many operations are required in the
updating phase as a function of the width parameter
-dimensional and they are compared by using Euclidean
metric. How many multiplication and adding operations are required for finding the
winning neuron. Calculate also how many operations are required in the
updating phase as a function of the width parameter 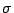 of the
neighborhood. Assume then that of
of the
neighborhood. Assume then that of 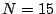 ,
, 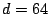 , and
, and 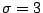 . Is it
computationally more demanding to find the winning neuron or update
the weights?
. Is it
computationally more demanding to find the winning neuron or update
the weights?
- The function
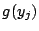 denotes a nonlinear function of the
response
denotes a nonlinear function of the
response 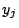 , which is used in the SOM algorithm as described in
Equation (9.9):
, which is used in the SOM algorithm as described in
Equation (9.9):
Discuss the implications of what could happen if the constant term in
the Taylor series of 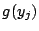 is nonzero. (Haykin, Problem 9.1)
is nonzero. (Haykin, Problem 9.1)
Jarkko Venna
2005-04-19
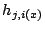 is a constant for all
is a constant for all 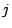 and
and 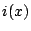 , and
, and
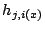 is the Kronecker delta function?
is the Kronecker delta function?