Tik-61.261 Principles of Neural Computing
Raivio, Venna
Exercise 10
- The thin-plate-spline function is described by
Justify the use of this function as a translationally and rotationally
invariant Green's function. Plot the function
graphically. (Haykin, Problem 5.1)
- The set of values given in Section 5.8 for the weight
vector
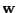 of the RBF network in Figure 5.6. presents one
possible solution for the XOR problem. Solve the same problem by
setting the centers of the radial-basis functions to
of the RBF network in Figure 5.6. presents one
possible solution for the XOR problem. Solve the same problem by
setting the centers of the radial-basis functions to
![$\displaystyle \mathbf{t}_1=[-1,1]^T$](img5.gif) and and ![$\displaystyle \mathbf{t}_2=[1,-1]^T.$](img6.gif) |
|
(Haykin, Problem 5.2)
- Consider the cost functional
which refers to the approximating function
Show that the cost functional
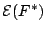 is minimized
when
is minimized
when
where the 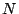 -by-
-by-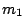 matrix
matrix
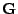 , the
, the 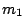 -by-
-by-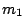 matrix
matrix
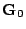 , the
, the 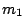 -by-1 vector
-by-1 vector
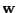 , and the
, and the 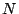 -by-1
vector
-by-1
vector
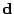 are defined by Equations (5.72), (5.75), (5.73), and
(5.46), respectively. (Haykin, Problem 5.5)
are defined by Equations (5.72), (5.75), (5.73), and
(5.46), respectively. (Haykin, Problem 5.5)
- Consider more closely the properties of the singular-value
decomposition (SVD) discussed very briefly in Haykin,
p. 300.
- Express the matrix
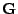 in terms of its singular values
and vectors.
in terms of its singular values
and vectors.
- Show that the pseudoinverse
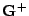 of
of
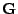 can be computed from Equation (5.152):
can be computed from Equation (5.152):
- Show that the left and right singular vector
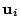 and
and
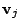 are obtained as eigenvectors of the matrices
are obtained as eigenvectors of the matrices
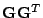 and
and
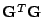 , respectively, and the
squared singular values are the corresponding nonzero eigenvalues.
, respectively, and the
squared singular values are the corresponding nonzero eigenvalues.
Jarkko Venna
2005-04-13
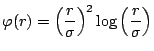 for some
for some ![$\displaystyle \mathcal{E}(F^{\ast}) = \sum_{i=1}^{N} \left[d_i-\sum_{j=1}^{m_1}...
...bf{x}_j -\mathbf{t}_i \Vert)\right]^2 + \lambda \Vert\mathbf{D}F^{\ast} \Vert^2$](img7.gif)
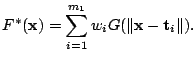
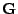 in terms of its singular values
and vectors.
in terms of its singular values
and vectors.
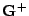 of
of
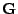 can be computed from Equation (5.152):
can be computed from Equation (5.152):
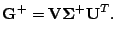
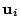 and
and
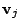 are obtained as eigenvectors of the matrices
are obtained as eigenvectors of the matrices
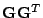 and
and
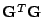 , respectively, and the
squared singular values are the corresponding nonzero eigenvalues.
, respectively, and the
squared singular values are the corresponding nonzero eigenvalues.