T-61.2010 Course assignment: #1 "Eigenfaces"
Using PCA to a collection of human face images.
Contents
- Preliminaries
- Introduction
- Documentation
- Some Matlab functions
- Image database
- (1) Reading face images to Matlab
- (2) Constructing data matrix
- (3) Principle component analysis (PCA)
- (4) Eigenfaces of dataset
- (5) Projecting images
- (6) Compression - projection to m-dimensional space
- (7) Decompression - back to d-dimensional space
- (8) Questions
Student
Student: Joe Doe
Student ID: 12345A
Preliminaries
Read about PCA and dimension reduction, look through "paper exercises" 1 and 2 from 2nd round, check how to compute with matrices and how to find eigenvalues, get familiar to Matlab.
Introduction
The target of this assignment is to demonstrate use of PCA in case of human faces.
For the assignment, a personalised Matlab data file, consisting of a set of gray scale images, can be accessed through the WWW pages of the course. Mail Ville.Viitaniemi at tkk.fi of you can not find a data set with your student number.
Your task is to:
- (1) draw all original face images.
- (2) convert the image file to a data matrix X by "scanning" images. The number of rows of X shall be the size of each image, that is, product of rows and columns in each picture. The number of columns of X is the number of data points, that is, different face images.
- (3) compute PCA: (3A) remove average, (3B) compute covariance matrix C_x, (3C) compute eigenvectors and eigenvalues of C_x.
- (4) draw "eigenfaces" = eigenvectors (number of images)
- (5) project the original faces (matrix X) using two eigenvectors e_i, which have biggest eigenvalues
- (6) project the original faces (matrix X) using m "biggest" eigenvectors e_i. d pixels sized image is now "compressed" to m values where m < d
- (7) show the projections as face images
- (8) answer the questions below
Keywords are "PCA - Principal Component Analysis" and "eigenfaces".
The code and documentation are to be written individually using the personal datasets. However, discussion in small groups or in news group is very welcome. Plagiarism is prohibited (CS department instructions regarding dealing with plagiarism apply.)
Documentation
You have to return a document and the code as attachments of email by 15.1.2008 to vvi@cis.hut.fi. Use subject: "T-61.2010 assignment #1 STUD_ID", where STUD_ID is replaced by your own student ID.
The document must contain the name, student ID and email address of the student, small description the phases of the assignment, your results and answers to the questions (8). Convert your document into PDF.
Copy your Matlab code into a file and include it as an email attachment.
Some Matlab functions
Some hints can be found from computer sessions, especially round #2.
There are some functions to be used:
- myMontage.m: similar to montage in Matlab
For matrices:
- help help on any matlab command
- doc richer documentation of the commands
- size size of a matrix
- min, max, sort minimum, maximum and sorting
- sum sum of elements of a vector
- reshape altering the size of a matrix
- repmat copying a matrix
- eig eigenvalue calculation
- diag picks values from diagonal of a matrix
- for i = [1:4], i*i, end; "for" loop
- if (i==4), j=0, else, j=1, end; "if" construct
- print saving an image as .png, .eps, .jpg, .tif, ...
- saveas saving an image as .png, .eps, .jpg, .tif, ...
In this work the data matrix consists of gray level images. Matlab Image Processing Toolbox (IPT) contains some useful functions ("doc images"):
- imread reading an image to Matlab
- montage drawing multiple images in the same window
- imshow drawing an image
- double converting matrix to contain data type double
- uint8 converting matrix to contain 8 bit unsigned integers
Image database
This assignment deals with human faces. There can be several images from each person. They are positioned, all images are 19x19 pixels.
Fetch your own personal image file XXXXXY.mat (Topic #1) through http://www.cis.hut.fi/Opinnot/T-61.2010/Harjoitustyo/.
The database CBCL is from MIT http://cbcl.mit.edu/cbcl/software-datasets/FaceData2.html
Copyright 2000. Center for Biological and Computational Learning at MIT and MIT. All rights reserved.
Permission to copy and modify this data, software, and its documentation only for internal research use in your organization is hereby granted, provided that this notice is retained thereon and on all copies. This data and software should not be distributed to anyone outside of your organization without explicit written authorization by the author(s) and MIT. It should not be used for commercial purposes without specific permission from the authors and MIT. MIT also requires written authorization by the author(s) to publish results obtained with the data or software and possibly citation of relevant CBCL reference papers.
We make no representation as to the suitability and operability of this data or software for any purpose. It is provided "as is" without express or implied warranty.
Example run
Variables used in the instructions below. The only variable you get from your personal data file is K.
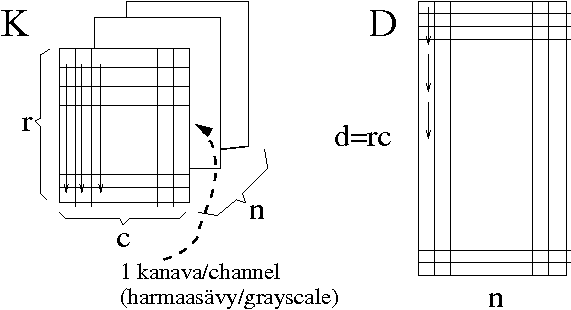
- K (r x c x 1 x n) 4-dimensional matrix of data type uint8 ("unsigned integer 8", 2^0 .. 2^8-1 i.e. integers 0 throgh 255, 0 correponding to black 255 wo white on a grey scale), consisting of
- r rows in each image
- c columns in each image
- n number of images
- X (rc x n) data matrix that is formed to contain all the images
- d size of X, i.e. d = rc
- C (rc x rc) Correlation matrix of X, denoted C_x in the course material
- V (rc x rc) eigenvectors of C (in columns), in this application: the eigenfaces
- D (rc x rc) on diagonal diag(D) eigenvalues lambda_i of C
- W (rc x 2) projection matrix to project X to the xy-plane to form matrix Y
- Y (2 x n) projection of X in 2 dimensions
- WM (rc x m) projection matrix to project X into a m-dimensional matrix||
- YM (m x n) projection of X in m dimensions
- XH (rc x n) reconstructed data matrix
- M (r x c x 1 x n) reconstructed 4-dimensional image matrix
(1) Reading face images to Matlab
Fetch your own file XXXXXY.mat (Topice #1) through URL http://www.cis.hut.fi/Opinnot/T-61.2010/Harjoitustyo/. (NOTE! Mail Ville.Viitaniemi () tkk.fi if you can not find data with your student number.
Read the file with load. Now you have n images in Matlab image matrix K. Images are gray scale, of same size (r rows and c columns). Using montage (or myMontage) you can draw all faces at the same time.
load([opnro '_train.mat']); % Tähän oma <opnro>, sisältää matriisin K r = size(K,1); c = size(K,2); n = size(K,4); datatype = class(K); disp(['Kuvia on ' num2str(n) ' kappaletta']); disp(['Kunkin kuvan koko on (' num2str(r) ' x ' num2str(c) ') ja tyyppi ' datatype]); myMontage(K, 'Alkuperäiset kuvat', 1);
Kuvia on 92 kappaletta Kunkin kuvan koko on (19 x 19) ja tyyppi uint8
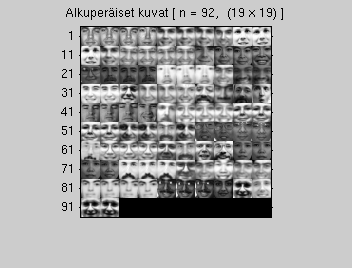
(2) Constructing data matrix
Modify (Cast) each image into double type and read each image into a column vector. Now you will have a matrix X (D) with d=rc rows and n columns.
(3) Principle component analysis (PCA)
Compute PCA. Remove the mean (size d x 1):
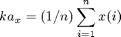
Substract the mean from the matrix. Then compute the covariance matrix (size d x d):
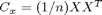
Finally, compute eigenvalues and eigenvectors from C_x using command eig. (Eigenvectors should be sorted according to eigenvalues.)
(4) Eigenfaces of dataset
Eigenfaces are now eigenvectors of C_x (columns). :n ominaisvektorit, jotka ovat matriisissa, jonka koko on (d x d). In order to draw eigenfaces with montage, one has to
- pick n eigenvectors (faces) whose corresponding eigenvalues are largests
- convert that matrix into image matrix L with size [r x c x 1 x n]
- scale values in range 0..255 and cast the data type into uint8

(5) Projecting images
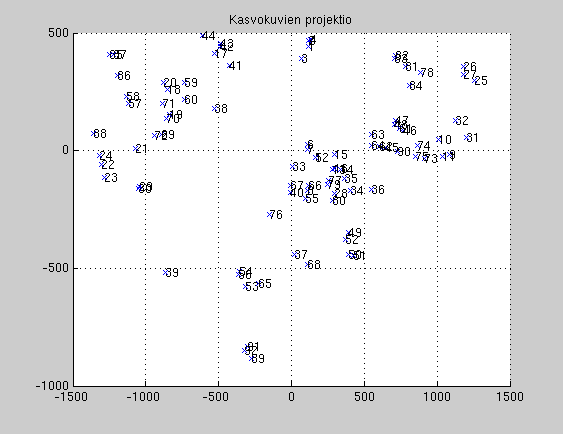
Project data points (faces) into a 2D-space spanned by two largest eigenvectors. The images looking similar should map close to each other.
Pick two eigenvectors whose eigenvalues are two largest. Let W contain these vectors (d x 2), and the projection is done using:
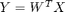
Y is (2 x n). Plot these n points in xy-space using plot(x,y,'x'), see "help plot". You can add text (numbers) with command text.
(6) Compression - projection to m-dimensional space
In this example the cumulative sum of eigenvalues is computed. The error J when leaving eigenvectors m..d out:
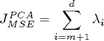
In this way you can choose a correct number of eigenvectors to be saved
1..d | index number | cum. sum %
1.0000 1.0000 54.9890
2.0000 2.0000 65.0714
3.0000 3.0000 71.6040
4.0000 4.0000 76.1306
5.0000 5.0000 79.4855
6.0000 6.0000 82.1150
7.0000 7.0000 84.4082
8.0000 8.0000 85.9933
9.0000 9.0000 87.2604
10.0000 10.0000 88.4974
11.0000 11.0000 89.5934
12.0000 12.0000 90.5740
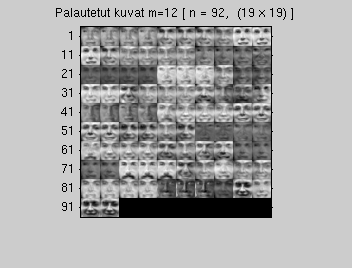
Compress data so that m first eigenvectors e_i are taken into account. Choose m so that 90 pro cent of variation (energy) is taken.
Valitaan m=12 ominaisvektoria, jotta saavutetaan 90%
In the compression the original figure is represented with vector p, whose dimension is only (m x 1). p expresses how great amount each eigenface is from total image. The total compression takes the matrix (m x n) and eigenvectors (d x m)

(7) Decompression - back to d-dimensional space
Decompress n vectors p (m values) back to images x_hat (each figure d = r x c pixels).
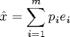
Modify the matrix and draw.
(8) Questions
Think through and answer to the following questions:
- If image is size is 19x19 and each pixel can have 256 gray scale values, what is the maximum of different possible images?
- Is the projection linear or not?
- Are the images which are almost same originally also near in 2D projection?
- How do points (faces images), which are far away in the projection, differ from each other?
- How many eigenfaces were needed so that at least 90% of variation was sustained?
- How did the recovered images differ from originals?