T-61.2010 Harjoitustyö: #1 "Ominaiskasvot"
Pääkomponenttianalyysin (PCA) käyttäminen kuva-aineistoon.
Sisältö
- Työn tekijä:
- Esitiedot
- Tehtäväkuvaus
- Dokumentointi
- Matlabin funktiota datan ja kuvien käsittelyyn
- Kuvatietokanta
- (1) Kasvokuvien lukeminen Matlabiin
- (2) Datamatriisin muodostaminen
- (3) Pääkomponenttianalyysin (PCA) laskeminen
- (4) Datasetin ominaiskasvot
- (5) Kasvokuvien kuvaaminen tasolle
- (6) Pakkaaminen - kuvien projektio m-ulotteiseen avaruuteen
- (7) Projektiopisteiden palauttaminen kuviksi d-avaruuteen
- (8) Pohdinnat
Työn tekijä:
Opiskelija: Matti Meikäläinen
Opiskelijanumero: 12345A
Sähköpostiosoite: mmeikala@cc.hut.fi
Esitiedot
Tehtävää varten on hyvä lukea luennon 4 aiheet PCA:sta ja dimensionaalisuuden pienentämisestä, lukea "paperilaskarien" PCA-tehtävät toiselta harjoituskierrokselta, kerrata matriisilaskun perusteet ja ominaisarvojen laskeminen sekä tutustua Matlabin käyttöön.
Tehtäväkuvaus
Tämän tehtävän tarkoituksena on demota luennoilla esitettyjä ominaiskasvoja ja PCA-projektiota.
Työtä varten jokaiselle opiskelijalle on kurssin WWW-sivuilla oma Matlab-tiedosto, josta ladataan joukko harmaasävyvalokuvia, jotka esittävät kasvoja. Jos datasettiä ei löyty, ota yhteyttä Ville Viitaniemeen, Ville.Viitaniemi at tkk.fi.
Tehtävänä on:
- (1) piirtää kaikki alkuperäiset kasvokuvat jatkoanalyysiä varten.
- (2) muokata kuvatiedosto datamatriisiksi X "skannaamalla" kuvat sarakkeittain (Matlabissa helpompi kuin riveittäin, ei vaikutusta tulokseen). X:n rivien määrä eli dimensio on nyt yksittäisen kuvan rivien ja sarakkeiden tulon määrä. X:n sarakkeiden määrä on datapisteiden eli kuvien määrä.
- (3) tehdä pääkomponenttianalyysi (PCA) datalle: (3A) poistaa keskiarvo jokaisesta dimensiosta, kts. esim. laskarien H2 / 1. (3B) laskea kovarianssimatriisi C_x, (3C) laskea C_x:n ominaisvektorit ja -arvot.
- (4) piirtää "ominaiskasvot" eli ominaisvektorit (kuvien lukumäärä)
- (5) projisoida alkuperäiset kasvokuvat eli matriisi X käyttämällä kahta ominaisvektoria e_i, joita vastaavat ominaisarvot ovat suurimmat
- (6) projisoida alkuperäiset kasvokuvat eli matriisi X käyttämällä m "suurinta" ominaisvektoria e_i, jolloin d-pikseliä suuri kuva "pakataan" m:ään arvoon, m < d
- (7) palauttaa edellisessä kohdassa tehty projektio takaisin kasvokuviksi (todennäköisesti huonompilaatuisia mutta toivon mukaan tunnistettavissa)
- (8) vastata pohdintaosiossa oleviin kysymyksiin
Asiaa on käsitelty datamatriisin tiivistämisen ja dekorreloinnin luennolla, luentokalvojen luvussa 4. Avainsanoja ovat "PCA - Principal Component Analysis" ja "eigenfaces".
Työ tehdään ja dokumentointi palautetetaan yksin oman datasetin pohjalta. Keskustelutasolla 1-3 hengen ryhmät voivat olla hyödyllisimpiä. Koodin kopiointi on kielletty T-osaston vilppitapausten toimintaohjeen mukaisesti: http://tieto.tkk.fi/vilppitoimintaohje.html
Dokumentointi
Tästä työstä tulee palauttaa dokumentti ja koodi sähköpostin liitteenä viimeistään 15.1.2008 sähköpostiosoitteeseen vvi@cis.hut.fi . Sähköpostin otsikoksi: "T-61.2010 harjoitustyo #1 OPNRO", jossa OPNRO korvataan omalla opiskelijanumerolla.
Viestissä pitää olla kaksi liitetiedostoa, joista ensimmäisessä liitteessä tulee olla työstä kirjoitettu dokumentti. Siitä pitää käydä ilmi työn tekijä, opiskelijanumero ja sähköpostiosoite, lyhyt selostus työn vaiheista ja tulokset kuvina. Mahdollinen yhteistyö sekä lähteet tulee mainita. Lopussa tulee vastata pohdintaosan (8) kysymyksiin. Tiedoston pitää olla PDF-muodossa ja nimetty muotoon "DT2007_HT1_doc_<opnro>.pdf" eli esimerkiksi "DT2007_HT1_doc_12345A.pdf".
Toisessa liitteessä on käytetty Matlab-koodi yhdessä ajokelpoissa tiedostossa (pääte .m), jonka muoto "DT2007_HT1_m_<opnro>.m", kuten yllä.
Matlabin funktiota datan ja kuvien käsittelyyn
Vinkkejä Matlabin yleiseen käsittelyyn löytyy myös kurssin tietokoneharjoituksista T#2 sekä Internetistä.
Kurssin www-sivulta löytyy myös apufunktioita:
- myMontage.m: sama kuin Matlabin montage, mutta lisää hieman luettavuutta
Matriisien käsittelyyn ja analysointiin:
- help apua kuhunkin komentoon
- doc laajempi dokumentaation komentoihin
- size matriisin koko
- min, max, sort minimi, maksimi ja järjestäminen
- sum vektorin summa alkioittain
- reshape matriisin koon muokkaaminen
- repmat matriisin kopioiminen
- eig ominaisarvojen laskeminen
- diag poimii arvot neliömatriisin diagonaalilta
- for i = [1:4], i*i, end; for-silmukka
- if (i==4), j=0, else, j=1, end; if-rakenne
- print kuvan tallettaminen .png, .eps, .jpg, .tif, ...
- saveas kuvan tallentaminen .png, .eps, .jpg, .tif, ...
Tässä työssä datamatriisi koostuu harmaasävykuvista. Matlabin Image Processing Toolbox (IPT) sisältää funktiota kuvien käsittelyyn. Ehkä parhaimman kuvan asiasta saa avaamalla Matlab ja etsimällä IPT:n johdannon tai kirjoittamalla "doc images".
Mukana on mm. funktioita:
- imread kuvan lukemiseen Matlabiin
- montage useamman kuvan piirtämiseen samaan ikkunaan
- imshow kuvan piirtämiseen
- double muutetaan double-tyyppiseksi matriisiksi
- uint8 muutetaan unsigned integer 8bit -tyyppiseksi
Kuvatietokanta
Tässä tehtävässä käsitellään eri ihmisten kasvokuvia. Yhdestä ihmisestä voi olla useampi erilainen kuva. Kasvokuva on rajattu varsin tarkasti ja silmien, nenän ja suun sijainti on kaikissa kuvissa suurinpiirtein samassa kohtaa. Kuvat ovat harmaasävykuvia ja samankokoisia. Ehdotetun menetelmän osalta kuvan koko täytyy olla "hyvin pieni".
Hae oma henkilökohtainen kuvatiedosto XXXXXY.mat (Aihe #1) osoitteesta http://www.cis.hut.fi/Opinnot/T-61.2010/Harjoitustyo/.
Käytetty kuvatietokanta on MIT:n tarjoama CBCL http://cbcl.mit.edu/cbcl/software-datasets/FaceData2.html
Copyright 2000. Center for Biological and Computational Learning at MIT and MIT. All rights reserved.
Permission to copy and modify this data, software, and its documentation only for internal research use in your organization is hereby granted, provided that this notice is retained thereon and on all copies. This data and software should not be distributed to anyone outside of your organization without explicit written authorization by the author(s) and MIT. It should not be used for commercial purposes without specific permission from the authors and MIT. MIT also requires written authorization by the author(s) to publish results obtained with the data or software and possibly citation of relevant CBCL reference papers.
We make no representation as to the suitability and operability of this data or software for any purpose. It is provided "as is" without express or implied warranty.
Tehtävänannossa käytettävät muuttujat
Seuraavassa tehtävänannossa käytettyjä muuttujia. Ainut muuttuja, jonka saat omasta datatiedostostasi, on K.
- K (r x c x 1 x n) 4-ulotteinen matriisi tyyppiä uint8 ("unsigned integer 8", 2^0 .. 2^8-1 eli kokonaisluvut 0 .. 255, jossa 0 vastaa mustaa ja 255 valkeaa harmaasävyasteikolla), sisältää
- r rivejä kussakin kuvassa
- c sarakkeita kussakin kuvassa
- n kasvokuvien lukumäärä
- X (rc x n) datamatriisi, joka koostetaan kasvokuvien kokoelmasta
- d X:n dimensio eli d = rc
- C (rc x rc) X:n korrelaatiomatriisi, materiaalissa C_x
- V (rc x rc) C:n ominaisvektorit sarakkeittain, tässä sovelluksessa ominaiskasvot
- D (rc x rc) diagonaalilla diag(D) C:n ominaisarvot lambda_i
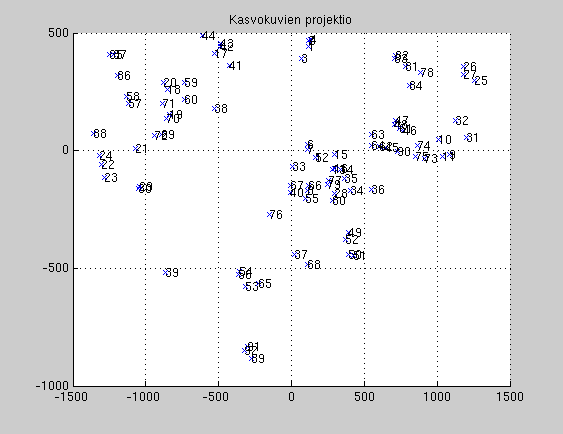
- W (rc x 2) projektiomatriisi, jolla X projisoidaan xy-tasoon matriisiksi Y
- Y (2 x n) X:n projektio W:lle
- WM (rc x m) projektiomatriisi, jolla X projisoidaan m-ulotteiseksi matriisiksi ||
- YM (m x n) X:n projektio WM:lle
- XH (rc x n) palautettu datamatriisi
- M (r x c x 1 x n) palautettu 4-ulotteinen kuvamatriisi
Esimerkkiajo
(1) Kasvokuvien lukeminen Matlabiin
Haetaan oma tiedosto XXXXXY.mat (Aihe #1) osoitteesta http://www.cis.hut.fi/Opinnot/T-61.2010/Harjoitustyo/. (HUOM! Jos tiedostoa ei ole olemassa, mailaa Ville.Viitaniemi miuku-mauku tkk fi, kirjoita viestiin opiskelijanumerosi ja pyydä tiedostoa.)
Luetaan tiedosto komennolla load. Näin on saatu luettua n kuvatiedostoa sisään Matlabin kuvamatriisiin K. Kuvat ovat harmaasävyskaalalla, samankokoisia (r riviä ja c saraketta) ja kuvan kohteet asemoitu. Komennolla montage voi piirtää kuvakokoelman kerralla (tai myMontage, katso yllä).
load([opnro '_train.mat']); % Tähän oma <opnro>, sisältää matriisin K r = size(K,1); c = size(K,2); n = size(K,4); datatype = class(K); disp(['Kuvia on ' num2str(n) ' kappaletta']); disp(['Kunkin kuvan koko on (' num2str(r) ' x ' num2str(c) ') ja tyyppi ' datatype]); myMontage(K, 'Alkuperäiset kuvat', 1);
Kuvia on 92 kappaletta Kunkin kuvan koko on (19 x 19) ja tyyppi uint8
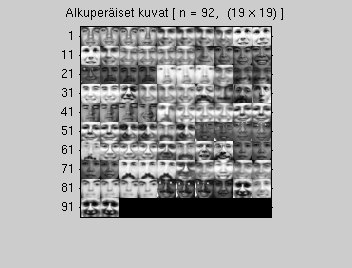
(2) Datamatriisin muodostaminen
Muokataan kukin kuva double-tyyppiseksi ja muodostetaan kustakin kuvasta yksi vektori yhdistämällä sarakkeet (luentokalvoissa riveittäin). Muodostetaan kaikkien kuvien vektoreista matriisi X, jonka rivimäärä on d=rc ja sarakemäärä n.
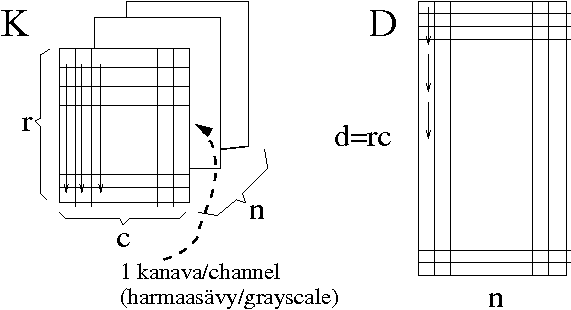
(3) Pääkomponenttianalyysin (PCA) laskeminen
PCA poistaa korrelaatiot vektorialkioiden välillä ja samalla löytää kierron vektoriavaruudessa siten, että uusilla koordinaateilla on maksimaalisen suuret varianssit.
Lasketaan PCA vaiheittain. Poistetaan ensin keskiarvo eli "datapilven" keskiarvo tulee nollaan eli käytännössä keskiarvo (koko d x 1):
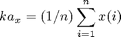
Vähennetään saatu keskiarvo matriisista. Haetaan sitten kovarianssimatriisi (koko d x d) laskemalla X:n ulkotulo:
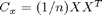
Lopuksi lasketaan ominaisarvot ja -vektorit matriisista C_x komennolla eig. Ominaisvektorit on hyödyllistä järjestää niitä vastaavien ominaisarvojen suuruusjärjestykseen.
(4) Datasetin ominaiskasvot
Ominaiskasvot ovat nyt C_x:n ominaisvektorit, jotka ovat matriisissa, jonka koko on (d x d). C_x:n ominaisarvot löytyvät matriisin D diagonaalilta (komento diag) ja ovat siis skalaareja. Piirretään ominaiskasvot komennolla montage, mitä varten pitää
- poimia n kappaletta suurimman ominaisarvon vastaavaa ominaisvektoria (== ominaiskasvoa)
- muokata kuvamatriisin L kooksi [r x c x 1 x n]
- tehdä skaalaus välille 0..255 ja muuttaa datatyyppi uint8:ksi

(5) Kasvokuvien kuvaaminen tasolle
Projisoidaan kaikki kuvat käyttäen kahta suurinta ominaisvektoria. Näin voidaan etsiä kuvien lähekkäisyys.
Poimitaan ominaisarvovektoreista ne kaksi, joiden ominaisarvot ovat suurimmat. Sisältäköön W nämä kaksi ominaisvektoria (d x 2), jolloin kuvat projisoidaan 2D-tasolle:
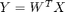
Y on siis (2 x n). Piirretään n pistettä xy-tasoon esimerkiksi komennolla plot(x,y,'x'), kts. "help plot". Tekstiä (numeroita) voi halutessaan lisätä komennolla text.
(6) Pakkaaminen - kuvien projektio m-ulotteiseen avaruuteen
Etsitään ensin ominaisarvojen kumulatiivinen summa (Aiemmin etsittiin ominaisarvojen suuruusjärjestys.) Tulostetaan kumulatiivinen summa ominaisarvoista. Pois jätettävistä ominaisarvoista saadaan virhe J
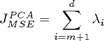
Näin ollen seuraavassa kohdassa voidaan valita sopiva määrä ominaisvektoreja mukaan.
jarj.nro | indeksinro | kumul.summa %
1.0000 1.0000 54.9890
2.0000 2.0000 65.0714
3.0000 3.0000 71.6040
4.0000 4.0000 76.1306
5.0000 5.0000 79.4855
6.0000 6.0000 82.1150
7.0000 7.0000 84.4082
8.0000 8.0000 85.9933
9.0000 9.0000 87.2604
10.0000 10.0000 88.4974
11.0000 11.0000 89.5934
12.0000 12.0000 90.5740
Kompressoidaan dataa siten, että otetaan m ensimmäistä (suurimmat ominaisarvot) ominaisvektoria e_i. m:n suuruus olkoon sellainen, että 90 prosenttia vaihtelusta otetaan mukaan.
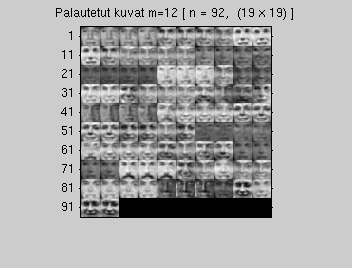
Valitaan m=12 ominaisvektoria, jotta saavutetaan 90%
Pakkauksessa kukin alkuperäinen kuva esitetään siis vektorilla p, jonka dimensio on (m x 1). p ilmaisee siis, mikä on kunkin ominaiskuvan osuus oikeasta kuvasta. Koko kuva-aineiston pakkaaminen vie siis matriisin (m x n) ja ominaiskuvat (d x m)

(7) Projektiopisteiden palauttaminen kuviksi d-avaruuteen
Palautetaan kaikki n kappaletta vektoreita p (m arvoa) takaisin kuviksi x_hattu (kukin kuva d = r x c pikseliä) .
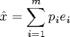
Muokataan matriisi kuvamuotoon takaisin ja piirretään.
(8) Pohdinnat
Pohdi seuraavia kohtia dokumentissasi:
- Jos kuvan koko on 19x19 ja kukin pikseli on voi saada 256 harmaasävyarvoa, niin mikä on mahdollisten erilaisten kuvien määrä?
- Onko projektiokuvaus lineaarinen vai epälineearinen?
- Ovatko alunperin toisiaan muistuttavat kuvat lähellä toisiaan myös 2D-projektiossa?
- Miten 2D-projektiossa kaukana toisistaan olevien pisteiden vastaavat kasvokuvat eroavat toisistaan?
- Kuinka monta ominaiskuvaa tarvitsit, jotta 90% vaihtelusta (ominaisarvojen summasta) jäi jäljelle?
- Millä tavoin palautetut kuvat erosivat alkuperäisistä? Miksi näin tapahtui?