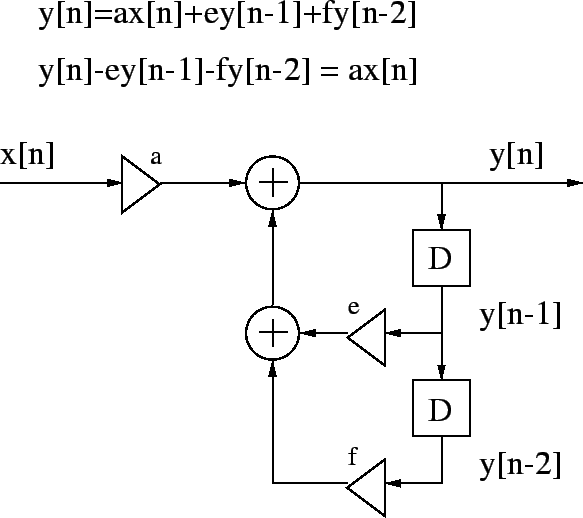![\begin{displaymath}\sum_{k=0}^N a_k \, y[n-k] = \sum_{k=0}^M b_k \, x[n-k]\end{displaymath}](img1.gif)
Block Diagrams / Lohkokaavio
A causal LTI system can be written with a differential equation
![\begin{displaymath}\sum_{k=0}^N a_k \, y[n-k] = \sum_{k=0}^M b_k \, x[n-k]\end{displaymath}](img1.gif)
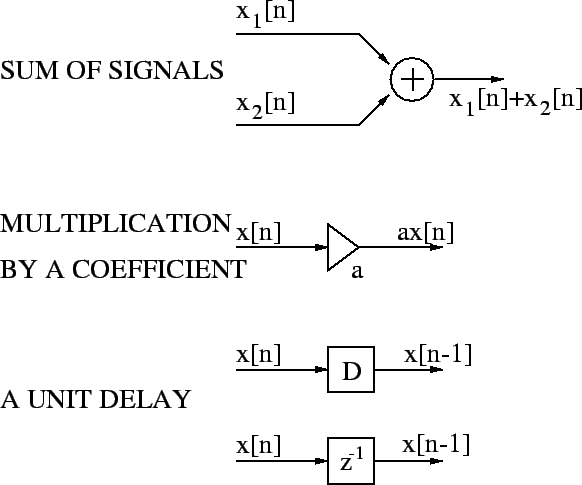
There are three basic functions in LTI systems.
FIR (finite impulse response) systems have an impulse response h[n]of finite length. For example
![]() is zero when n<0 or n>1. FIRs are therefore always BIBO-stable.
Transfer function H(z) consists only of numerator polynomial.
is zero when n<0 or n>1. FIRs are therefore always BIBO-stable.
Transfer function H(z) consists only of numerator polynomial.
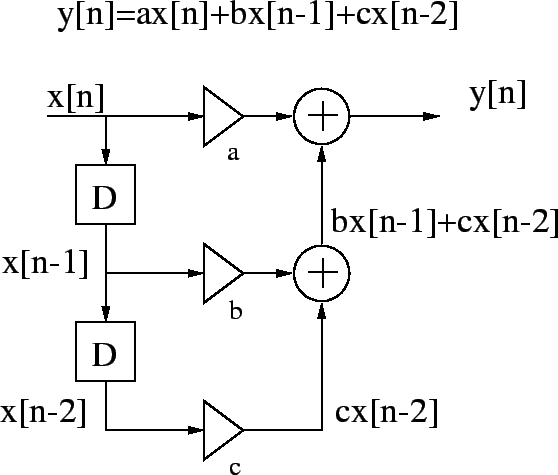
IIR (infinite impulse response) systems have an impulse response h[n]of infinite length. For example
h[n] = 0.5n u[n]is nonzero when ![]() .
IIRs contain feedback loops.
Transfer function H(z) consists of numerator and denominator
polynomials
.
IIRs contain feedback loops.
Transfer function H(z) consists of numerator and denominator
polynomials
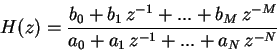
Stability can be derived from positions of poles (roots of denominator). If poles are strictly inside unit circle, then system is stable.