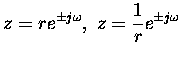Answers to Exercise 3. Mon, 2.10.2000: 17-20
Zero-pole diagram. Transfer function. Inverse
Tik-61.146 Digital Signal Processing and Filtering
(DISKO)
Answers to Exercise 3. Mon, 2.10.2000: 17-20
Zero-pole diagram. Transfer function. Inverse ![]() -transform. Stability
considerations. Minimum and maximum-phase transfer functions.
-transform. Stability
considerations. Minimum and maximum-phase transfer functions.
Start from the point (1,0), that is,
![]() .
Let
.
Let ![]() grow from 0 to
grow from 0 to ![]() on the unit circle
on the unit circle
![]() .
.
![]() is an even function (you can test symmetry
when
is an even function (you can test symmetry
when ![]() goes from 0 to
goes from 0 to ![]() ). The magnitude response can be
calculated or estimated roughly from
). The magnitude response can be
calculated or estimated roughly from
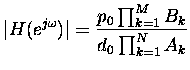
where ![]() are lengths of ``zero vectors'' and
are lengths of ``zero vectors'' and ![]() lengths of
``pole vectors''. From the equation it is seen that
zeros near (or on) the circle decrease the magnitude,
poles (inside the unit circle) increase it. All poles inside
the unit circle means that filter is causal and stable.
lengths of
``pole vectors''. From the equation it is seen that
zeros near (or on) the circle decrease the magnitude,
poles (inside the unit circle) increase it. All poles inside
the unit circle means that filter is causal and stable.
The magnitude is often expressed in desibels (dB).
Matlab uses in its plots desibels of
![]() :
:
Three filters:

Let us use Matlab to aid in solving this exercise. Compare these with the problem 8 in exercise round 2.
Using Matlab:
num = [1 -1.6 1]; den = [1 -1.2 0.52];
[z,p,k] = tf2zp(num,den);
Zeros are at
![]() and poles at
and poles at
![]() .
.
zplane(num,den) plots pole-zero-diagram, see the
figure 5.
Calculating magnitude reponse using Matlab
conv([1 -1.6 1],[1 -1.6 1]) for numerator and
conv([1 -1.2 0.52],[0.52 -1.2 1]) for denumerator
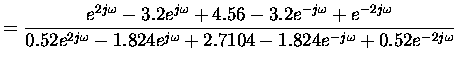
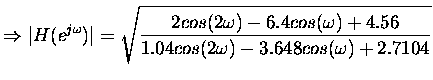
Using Matlab
cos1omega = cos([0:pi/256:pi]);
cos2omega = cos(2*[0:pi/256:pi]);
numvalues = sqrt(2*cos2omega - 6.4*cos1omega +4.56);
denvalues = sqrt(1.04*cos2omega - 3.648*cos1omega +2.7104);
values = numvalues./denvalues;
figure, subplot(211), plot([0:pi/256:pi], values); grid;
subplot(212), plot([0:pi/256:pi], 20*log10(values)); grid; ylabel('dB');
Magnitude
![]() and phase reponse
and phase reponse
![]() directly using
Signal Processing Toolbox of Matlab
freqz(num,den).
directly using
Signal Processing Toolbox of Matlab
freqz(num,den).
See the Figure 5.
Using Matlab:
[h,t]=impz(num,den);
stem(t,h);
See the Figure 6.
Let us begin by reviewing some properties we need in this exercise:
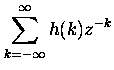 |
(2) |
First we have to solve the poles and zeros:
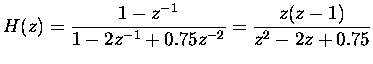
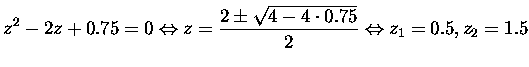
Zeros:
Now we may answer to the questions about stability and causality:
Note, that in this case we can't have a filter that is both causal and stable.
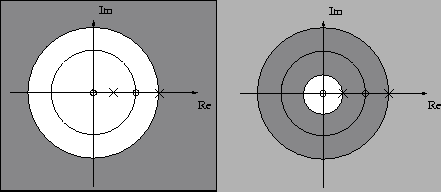 |
When we calculate the impulse response ![]() we have to do an inverse
we have to do an inverse
![]() -transformation for the transfer function
-transformation for the transfer function ![]() . To do this we
express the
. To do this we
express the ![]() as a partial fraction expansion as then we may
apply the formula of the sum of a geometric series (1).
as a partial fraction expansion as then we may
apply the formula of the sum of a geometric series (1).
Using the poles and zeros we may write the transfer function as follows:
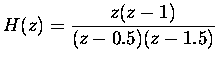
In a partial fraction expansion the degree of the nominator
polynomial has to be smaller than the degree of the denominator
polynomial. To achieve this, we by divide both by ![]() and do the
expansion in reference to
and do the
expansion in reference to ![]() (
(
![]() ):
):
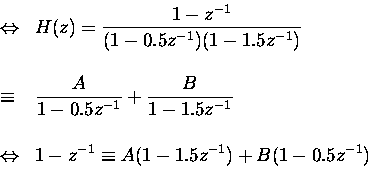
We solve ![]() and
and ![]() by letting
by letting
![]() and
and
![]()
![\begin{displaymath}
\begin{array}{ll}
z\rightarrow0.5: & 1-0.5^{-1} = A(1-1.5\cd...
...ot1.5^{-1}) \\ [8mm]
\Rightarrow & B=0.5 \\ [8mm]
\end{array}\end{displaymath}](img54.gif)
Now we may write the expansion
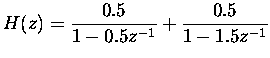
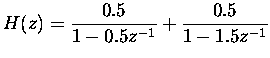
![\begin{displaymath}
\begin{array}{ll}
& \displaystyle 0.5\cdot\frac{1}{1-1.5z^{...
...nfty}\left(\frac{2}{3}\right)^{-m-1}\mu[-m-1]z^{-m}
\end{array}\end{displaymath}](img62.gif)
Thus, the inverse transform is
![$\displaystyle -\frac{1}{3}\left(\frac{2}{3}\right)^{-n-1}\mu[-n-1]
$](img63.gif)
and finally
![$\displaystyle h[n]=0.5\cdot0.5^n\mu[n]-\frac{1}{3}\left(\frac{2}{3}\right)^{-n-1}\mu[-n-1]
$](img64.gif)
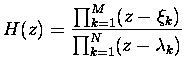
where zeros
![]() and poles
and poles
![]() and
and
![]() .
.
![$\displaystyle = \frac{\left((z-e^{j\pi/4})(z+e^{j\pi/4})\right)\left((z+e^{-j\p...
....5})(z+\sqrt[4]{0.5})\right)\left((z-\sqrt[4]{0.5}j)(z+\sqrt[4]{0.5}j)\right)} $](img70.gif)
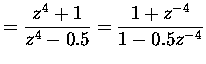
We want that the maximum magnitude is 1. From the
magnitude response (figure 4)
we see that
![]() is in its maximum, when
is in its maximum, when
![]() ,
for example
,
for example
![]() .
.
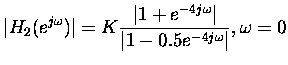
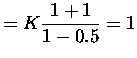
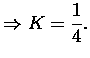
Filters are often normalized to unity for seeing better their properties instead of maximum magnitude.
In a common case scaling factor is
![]() ,
now
,
now ![]() . Comb filter realization without the scaling factor K
is shown in figure
. Comb filter realization without the scaling factor K
is shown in figure ![]() .
.
The part ![]() of the coefficient can be implemented
as follows:
of the coefficient can be implemented
as follows:
Division by two can be done using a bit shift. Shift operation (one bit to the right) is denoted here by symbol:
When we add the coefficient
![]() to the
realization, we can combine the multiplications by
to the
realization, we can combine the multiplications by ![]() into one:
into one:
![$\displaystyle \mathcal{S}=\sum^\infty_{n=-\infty}\vert h[n]\vert<\infty.$](img92.gif)
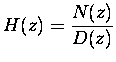
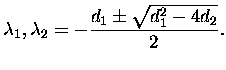
Now the poles can be either complex or real.
Then we check the condition for the second coefficient ![]() . Now
. Now
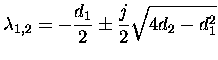
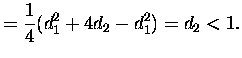
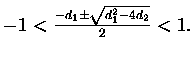 We analyze the above inequality piecewise, first the left hand side:
We analyze the above inequality piecewise, first the left hand side:
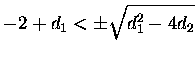
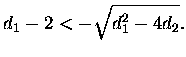
Then the right hand side:
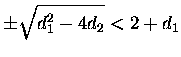
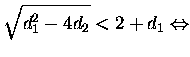
Stability triangle is the triangle the derived conditions form in the ![]() -plane. In the figure 9 is a visualization of the stability triangle.
-plane. In the figure 9 is a visualization of the stability triangle.
This results that the zeros must have the following symmetry: